Zadanie nr 6611774
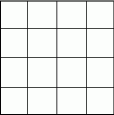
Na rysunku przedstawiono kwadratową tablicę 4x4 składającą się z 16 kwadracików jednostkowych. Ile jest równa największa możliwa liczba przekątnych, jakie można poprowadzić w tych kwadracikach jednostkowych w ten sposób, aby żadne dwie z nich nie przecinały się, ani nie miały wspólnych końców?
A) 8 B) 9 C) 10 D) 11 E) 12
Rozwiązanie
Chwilę kombinując można znaleźć układ z 10 przekątnymi (obrazek).
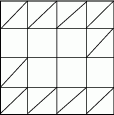
Aby wykazać, że układ ten jest maksymalny, wystarczy zauważyć, że w każdych dwóch sąsiednich rzędach muszą być co najmniej 3 puste kwadraciki (a więc całym kwadracie musi być co najmniej 6 pustych).
Sprowadziliśmy zatem sytuację do prostszego przypadku, gdy mamy 8 kwadracików (2 rzędy po 4). Załóżmy, że istnieje konfiguracja w tej figurze z dwoma pustymi kwadracikami. Łatwo zobaczyć, że nie mogą być one w jednym wierszu (bo wtedy drugi wiersz jest cały wypełniony i nie da się dorysować dwóch przekątnych - rysunek).

Ponadto, wokół każdego z trzech wewnętrznych wierzchołków musi być pusty kwadrat (bo nie da się wypełnić wszystkich sąsiadujących z takim wierzchołkiem kwadratów). Zatem konfiguracja pustych kwadratów jest jak w prawej części rysunku. W tej sytuacji też łatwo zobaczyć, że jedyny sposób dorysowania przekątnych w lewej czwórce to tak, że jedna z nich wchodzi w środkowy wierzchołek figury, ale wtedy nie da się wypełnić prawej czwórki.
Odpowiedź: C

