Zadanie nr 6767023
W czworokącie 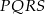 mamy
mamy 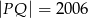 ,
, 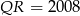 ,
, 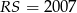 ,
, 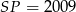 . Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż
. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 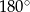 ?
?
A) 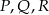 B)
B) 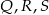 C)
C) 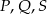 D)
D) 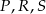 E)
E) 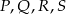
Rozwiązanie
Zauważmy, że gdy mamy czworokąt o bokach 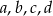 , który ma kąt większy od
, który ma kąt większy od 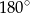 jak na obrazku, to
jak na obrazku, to 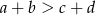 .
.
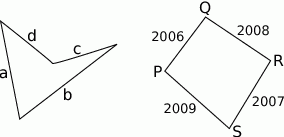
Najprościej sobie to wyobrazić, gdy myślimy, że wyprostowujemy ten jeden kąt większy od 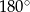 . Dostaniemy wtedy trójkąt z bokami
. Dostaniemy wtedy trójkąt z bokami 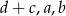 . Jest też, na odwrót, jeżeli w czworokącie mamy
. Jest też, na odwrót, jeżeli w czworokącie mamy 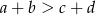 , to można zmienić ten czworokąt tak, aby kąt pomiędzy bokami długości
, to można zmienić ten czworokąt tak, aby kąt pomiędzy bokami długości  i
i 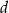 był większy od
był większy od 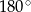 – aby to sobie wyobrazić, znowu należy sobie myśleć, że przechodzimy przez trójkąt o bokach
– aby to sobie wyobrazić, znowu należy sobie myśleć, że przechodzimy przez trójkąt o bokach 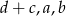 (prostujemy kąt między
(prostujemy kąt między  i
i 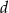 ).
).
Musimy więc popatrzeć dla których z boków naszego czworokąta zachodzi taki warunek. Ja się przyjrzymy, to mamy tylko jedną taką możliwość:
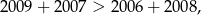
która odpowiada kątowi przy wierzchołku 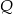 .
.
Odpowiedź: D

