Zadanie nr 7253051
Dwa wzajemnie styczne okręgi o równych promieniach mają środki w dwóch przeciwległych wierzchołkach kwadratu. Kolejne dwa okręgi, o środkach w pozostałych wierzchołkach kwadratu, są styczne zewnętrznie do każdego z dwóch poprzednich okręgów (patrz rysunek). Ile razy promień większego okręgu jest większy od promienia mniejszego okręgu?
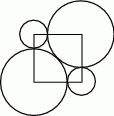
A) 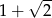 B)
B) 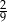 C)
C) 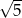 D)
D) 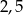 E)
E) 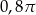
Rozwiązanie
Powiedzmy, że dany kwadrat ma bok długości 1.
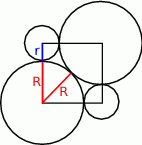
Promień większego okręgu to dokładnie połowa długości przekątnej kwadratu, czyli 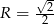 . Natomiast promień
. Natomiast promień  mniejszego okręgu spełnia równanie
mniejszego okręgu spełnia równanie
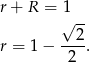
Zatem szukany iloraz jest równy
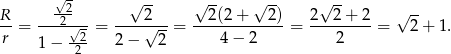
Odpowiedź: A

