Zadanie nr 7280492
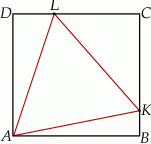
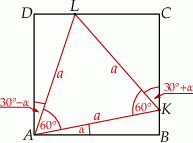
W prostokąt  wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny  (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek  leży na boku
leży na boku  (
(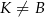 i
i 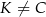 ), wierzchołek
), wierzchołek 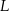 leży na boku
leży na boku 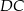 (
(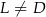 i
i 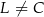 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 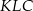 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 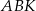 i
i 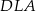 .
.
Rozwiązanie
Oznaczmy 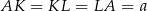 i
i 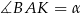 .
.
Mamy wtedy
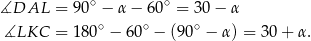
Spróbujemy teraz obliczyć pola wszystkich trzech trójkątów z treści zadania w zależności od  i
i  (powinno być jasne, że te dwa parametry jednoznacznie wyznaczają długości pozostałych odcinków na rysunku). Najpierw trójkąt
(powinno być jasne, że te dwa parametry jednoznacznie wyznaczają długości pozostałych odcinków na rysunku). Najpierw trójkąt 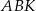 .
.
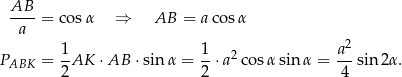
Teraz trójkąt 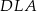 .
.
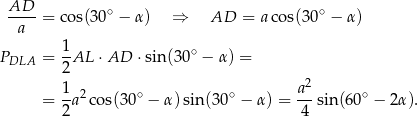
Analogicznie liczymy pole trójkąta 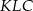 .
.
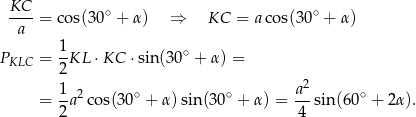
Mamy zatem
![a2 a2 a2 PABK + PDLA = ---sin2α + --sin(6 0∘ − 2 α) =---[sin 2α + sin(60∘ − 2α )] = 42 4 ∘ 4 ∘ a-- 2α-+--60-−--2α 2-α−--(60-−--2α) = 4 ⋅2 sin 2 cos 2 = a2 a2 1 = ---⋅2 sin 30∘ cos(2α − 30∘ ) = ---⋅2⋅ --cos(30∘ − 2α) = 4 4 2 a2- ∘ ∘ a2- ∘ = 4 cos (90 − (60 + 2α)) = 4 sin(60 + 2α ) = PKLC .](https://img.zadania.info/zad/7280492/HzadR12x.gif)

