Zadanie nr 7702348
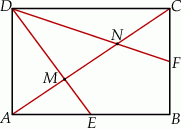
W prostokącie 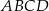 wierzchołek
wierzchołek 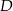 połączono odcinkami ze środkami
połączono odcinkami ze środkami 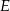 i
i 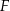 boków
boków 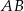 i
i 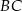 , zaś
, zaś 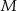 i
i 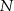 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 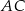 .
.
- Uzasadnij, że odcinki
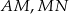 i
i 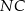 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
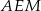 i
i 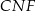 mają równe pola.
mają równe pola.
Rozwiązanie
Sposób I
Dorysujmy drugą przekątną prostokąta.
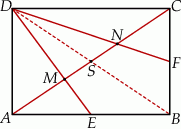
- Ponieważ przekątne prostokąta dzielą się na połowy, odcinki
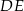 i
i 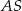 są środkowymi trójkąta
są środkowymi trójkąta 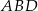 . Ponieważ środkowe dzielą się w stosunku 2:1 (licząc od wierzchołka), mamy
. Ponieważ środkowe dzielą się w stosunku 2:1 (licząc od wierzchołka), mamy 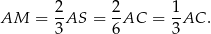
Podobnie, patrząc na trójkąt
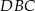 , uzasadniamy, że
, uzasadniamy, że 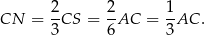
Zatem każdy z odcinków
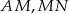 i
i 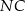 jest równy
jest równy 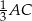 .
. - Trójkąty
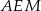 i
i 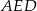 mają wspólną podstawę
mają wspólną podstawę 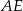 , a ich wysokości mają się jak
, a ich wysokości mają się jak 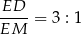
(twierdzenie Talesa). Zatem
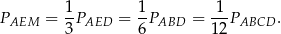
Podobnie dla trójkąta
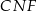 .
. 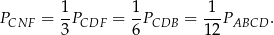
Sposób II
- Tym razem nie będziemy nic dorysowywać (patrzymy na oryginalny rysunek). Trójkąty
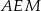 i
i 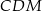 mają równe kąty, są więc podobne. W dodatku skala ich podobieństwa to
mają równe kąty, są więc podobne. W dodatku skala ich podobieństwa to 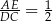 . Zatem
. Zatem 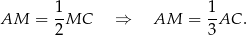
Podobnie, patrząc na trójkąty podobne
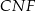 i
i  mamy
mamy 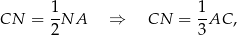
co kończy dowód.
- Z opisanego wyżej podobieństwa, wystarczy wykazać, że trójkąty
 i
i  mają równe pola. Oba te trójkąty mają jednak równe podstawy
mają równe pola. Oba te trójkąty mają jednak równe podstawy 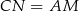 oraz wspólną wysokość, która jest na nie opuszczona.
oraz wspólną wysokość, która jest na nie opuszczona.

