/Konkursy

Zadanie nr 7853047

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie pary liczb całkowitych dodatnich 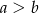a > b , dla których

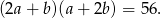
(2a+ b)(a+ 2b) = 56 .

Rozwiązanie

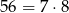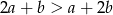Zauważmy, że 56 = 7 ⋅8 oraz 2a+ b > a + 2b . Dana równość może więc zachodzić w jednym z następujących 4 przypadków.

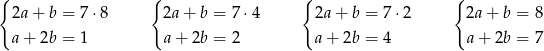
{ { { { 2a + b = 7 ⋅8 2a+ b = 7 ⋅4 2a + b = 7⋅ 2 2a + b = 8 a + 2b = 1 a+ 2b = 2 a + 2b = 4 a + 2b = 7

W każdym z przypadków odejmujemy od pierwszego równania drugie pomnożone przez 2 i otrzymujemy kolejno

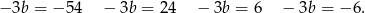
− 3b = − 54 − 3b = 24 − 3b = 6 − 3b = − 6.

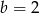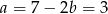Tylko w ostatnim przypadku otrzymujemy nieujemną wartość b = 2 . Wtedy a = 7− 2b = 3 .  
Odpowiedź: (a,b) = (3 ,2)

Wersja PDF