Zadanie nr 8156810
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 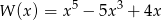 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
Rozwiązanie
Musimy rozłożyć podany wielomian na czynniki i pokazać, że dzielą się one przez 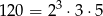 .
.
Rozkładamy
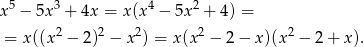
Rozkładamy teraz wielomiany kwadratowe w nawiasach, pierwiastki pierwszego (liczymy z 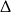 -y) to -1 i 2, a pierwiastki drugiego to 1 i -2. Mamy zatem
-y) to -1 i 2, a pierwiastki drugiego to 1 i -2. Mamy zatem
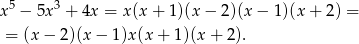
Jeżeli  jest liczbą naturalną to otrzymane wyrażenie jest iloczynem pięciu kolejnych liczb całkowitych. Wśród tych pięciu kolejnych liczb na pewno jest jedna podzielna przez 3 i jedna podzielna przez 5. Musimy jeszcze policzyć dwójki. Wśród tych pięciu liczb jest co najmniej jedna podzielna przez 4 i oprócz tego jeszcze jedna parzysta. Iloczyn dzieli się więc przez 8.
jest liczbą naturalną to otrzymane wyrażenie jest iloczynem pięciu kolejnych liczb całkowitych. Wśród tych pięciu kolejnych liczb na pewno jest jedna podzielna przez 3 i jedna podzielna przez 5. Musimy jeszcze policzyć dwójki. Wśród tych pięciu liczb jest co najmniej jedna podzielna przez 4 i oprócz tego jeszcze jedna parzysta. Iloczyn dzieli się więc przez 8.

