Zadanie nr 8227244
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Rozwiązanie
Rozpoczynamy od rysunku.
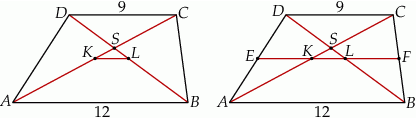
Sposób I
Zauważmy, że trójkąty 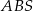 i
i 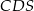 są podobne (maja równe kąty) i skala ich podobieństwa jest równa
są podobne (maja równe kąty) i skala ich podobieństwa jest równa
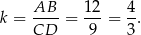
Stąd
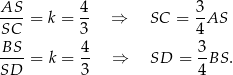
To pozwala obliczyć jaką cześć przekątnych 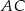 i
i 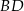 stanowią odcinki
stanowią odcinki 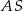 i
i 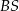 .
.
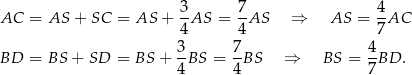
Z drugiej strony 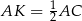 i
i 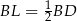 . Stąd
. Stąd
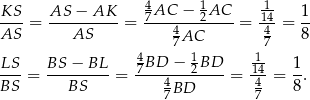
Trójkąt 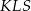 jest więc podobny do trójkąta
jest więc podobny do trójkąta 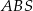 w skali 1:8. Stąd
w skali 1:8. Stąd
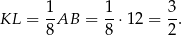
Sposób II
Niech 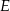 i
i 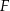 będą punktami wspólnymi prostej
będą punktami wspólnymi prostej 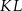 (przechodzącej przez środki przekątnych) i ramion trapezu. Zauważmy, że na mocy twierdzenia Talesa
(przechodzącej przez środki przekątnych) i ramion trapezu. Zauważmy, że na mocy twierdzenia Talesa
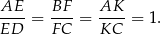
Punkty 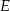 i
i 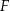 są więc środkami ramion trapezu. W takim razie odcinek
są więc środkami ramion trapezu. W takim razie odcinek 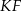 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 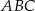 . Stąd
. Stąd
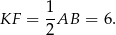
Podobnie, odcinek 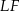 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 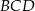 . Stąd
. Stąd
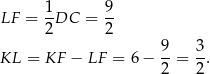
Sposób III
Tak jak w poprzednim sposobie zauważamy, że przedłużenie odcinka 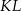 przecina ramiona trapezu w ich środkach
przecina ramiona trapezu w ich środkach 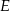 i
i 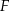 . Jak wiadomo odcinek
. Jak wiadomo odcinek 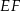 ma długość
ma długość 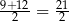 . Odcinki
. Odcinki 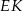 i
i 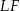 są odcinkami łączącymi środki boków odpowiednio w trójkątach
są odcinkami łączącymi środki boków odpowiednio w trójkątach 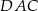 i
i 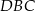 . Zatem
. Zatem 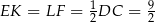 . Mamy zatem
. Mamy zatem
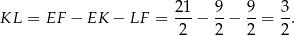
Odpowiedź: 

