/Konkursy

Zadanie nr 8248810

Dodaj do ulubionych
Dodaj do rozwiązanych

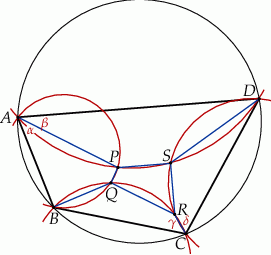
Przez każde dwa sąsiednie wierzchołki czworokąta 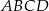ABCD wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).

PIC

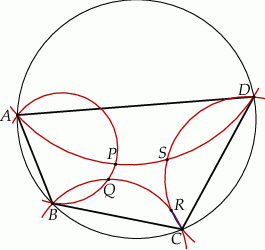
Wykaż, że punkty 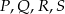P ,Q,R ,S , w których przecinają się te okręgi, leżą na jednym okręgu.

Rozwiązanie

Dorysujmy odcinki 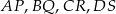AP ,BQ ,CR ,DS oraz boki czworokąta PQRS .

PIC

Oznaczmy ponadto 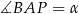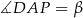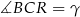∡BAP = α , ∡DAP = β , ∡BCR = γ i ∡DCR = δ .

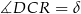Czworokąt 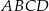ABCD jest wpisany w okrąg, więc

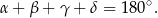
α + β + γ + δ = 180∘.

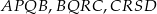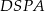Patrzymy teraz na czworokąty AP QB ,BQRC ,CRSD i DSPA . Każdy z nich jest wpisany w okrąg, więc

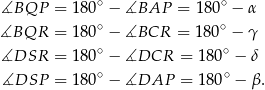
∡BQP = 180∘ − ∡BAP = 180∘ − α ∘ ∘ ∡BQR = 180 − ∡BCR = 180 − γ ∡DSR = 180∘ − ∡DCR = 180∘ − δ ∘ ∘ ∡DSP = 180 − ∡DAP = 180 − β .

Teraz łatwo już obliczyć miary dwóch przeciwległych kątów w czworokącie 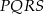P QRS .

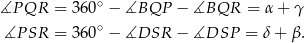
∘ ∡P QR = 360 − ∡BQP − ∡BQR = α + γ ∡P SR = 360∘ − ∡DSR − ∡DSP = δ + β.

Jak zauważyliśmy wcześniej

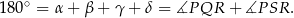
180∘ = α + β + γ + δ = ∡P QR + ∡P SR .

To oznacza, że na czworokącie 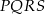P QRS można opisać okrąg.

Wersja PDF