Zadanie nr 8251843
Wykaż, że 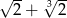 jest liczbą niewymierną.
jest liczbą niewymierną.
Rozwiązanie
Będziemy chcieli skorzystać z twierdzenia o wymiernych pierwiastkach wielomianów o współczynnikach. Aby to zrobić spróbujemy znaleźć wielomian o współczynnikach całkowitych, którego pierwiastkiem jest podana liczba. Liczymy.
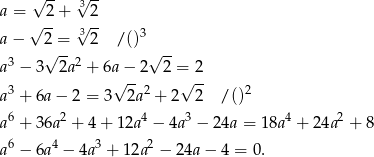
Na mocy twierdzenia o wymiernych pierwiastkach wielomianu o współczynnikach wymiernych, jeżeli 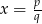 jest pierwiastkiem wymiernym tego wielomianu, to
jest pierwiastkiem wymiernym tego wielomianu, to 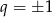 i
i 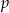 dzieli 4. To znaczy, że każdy pierwiastek wymierny tego wielomianu jest całkowity. Ponieważ jednak
dzieli 4. To znaczy, że każdy pierwiastek wymierny tego wielomianu jest całkowity. Ponieważ jednak
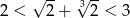
liczba  nie jest liczbą całkowitą. To dowodzi, że
nie jest liczbą całkowitą. To dowodzi, że  nie może być liczbą wymierną.
nie może być liczbą wymierną.

