/Konkursy

Zadanie nr 9592524

Dodaj do ulubionych
Dodaj do rozwiązanych

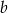Wykaż, że jeżeli liczby dodatnie a i b spełniają warunek

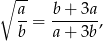
∘ -- a-= b-+-3a-, b a + 3b

to 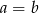a = b .

Rozwiązanie

Sposób I

Przekształcamy daną równość.

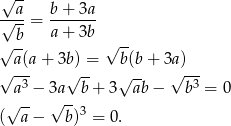
√a-- b + 3a √---= ------- b a + 3b -- √a-(a + 3b) = √ b(b+ 3a) √ --- √ -- √ -- √ --- a3 − 3a b + 3 ab − b 3 = 0 √ -- √ -- ( a − b)3 = 0.

Otrzymana równość oczywiście oznacza, że 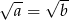√ -- √ -- a = b , czyli a = b .

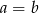Sposób II

Przekształcamy daną równość.

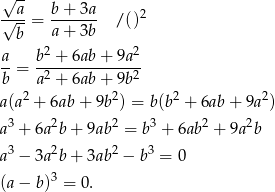
√a-- b + 3a √---= ------- /()2 b a + 3b a b2 + 6ab + 9a2 --= -2-----------2- b a + 6ab + 9b a(a2 + 6ab + 9b2) = b(b2 + 6ab+ 9a2) 3 2 2 3 2 2 a + 6a b + 9ab = b + 6ab + 9a b a3 − 3a2b + 3ab2 − b3 = 0 3 (a − b) = 0.

Zatem rzeczywiście 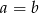a = b .

Wersja PDF