/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Różne

Zadanie nr 2241287

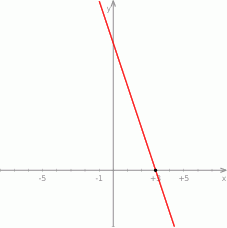
Na poniższym wykresie przedstawiono wykres pochodnej 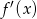′ f (x) funkcji kwadratowej 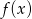f(x ) . Wykaż, że f(5) < f(2) .

PIC

Wersja PDF

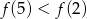Rozwiązanie

Sposób I

Z podanego wykresu pochodnej widać, że funkcja 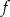f ma maksimum lokalne w 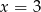x = 3 . To oznacza, że wykresem funkcji 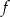f jest parabola o ramionach skierowanych w dół i wierzchołku, którego pierwsza współrzędna jest równa 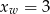x = 3 w . To oznacza, że prosta 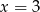x = 3 jest osią symetrii tej paraboli, czyli np.

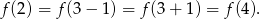
f(2 ) = f(3 − 1) = f (3+ 1 ) = f(4).

Wiemy ponadto (z wykresu pochodnej), że 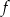f maleje dla 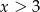x > 3 , więc

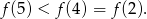
f(5) < f (4) = f(2).

Sposób II

Tak jak w poprzednim sposobie zauważmy, że pierwsza współrzędna wierzchołka paraboli będącej wykresem 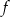f jest równa 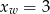xw = 3 . To oznacza, że 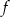f ma postać

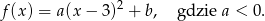
f(x) = a(x− 3)2 + b, gdzie a < 0.

Próbujemy teraz przekształcić nierówność, którą mamy udowodnić.

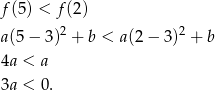
f (5) < f(2) 2 2 a(5 − 3 ) + b < a(2− 3) + b 4a < a 3a < 0.

Ta nierówność jest oczywiście spełniona, więc wyjściowa nierówność też musiała być prawdziwa (bo przekształcaliśmy przy pomocy równoważności).

Wersja PDF