/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne/Różne

Zadanie nr 9330184

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź wzór na sumę 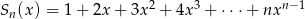2 3 n− 1 Sn(x) = 1+ 2x + 3x + 4x + ⋅⋅⋅+ nx .

Rozwiązanie

Sposób I

Popatrzmy na następujący układ jednomianów

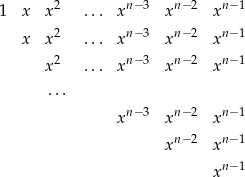
2 n− 3 n−2 n− 1 1 x x ... x x x x x 2 ... xn− 3 xn−2 xn− 1 2 n− 3 n−2 n− 1 x ... x x x ... xn− 3 xn−2 xn− 1 n−2 n− 1 x x xn− 1

Jeżeli przesumujemy wszystkie elementy tablicy sumując najpierw kolumny to widać, że suma ta jest równa 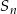Sn . Jeżeli natomiast będziemy patrzeć na wiersze to mamy ciągi geometryczne o ilorazie x . Sumy w wierszach wynoszą odpowiednio

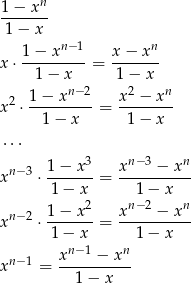
1 − xn ------- 1− x 1-−-xn−-1 x-−-xn- x ⋅ 1− x = 1− x n−2 2 n x2 ⋅ 1−-x----= x--−-x-- 1− x 1 − x ... 3 n− 3 n n− 3 1-−-x-- x----−--x- x ⋅ 1− x = 1 − x 1 − x2 xn− 2 − xn xn− 2 ⋅------= ---------- 1− x 1 − x n− 1 xn− 1 − xn x = ---------- 1 − x

Pozostało dodać do siebie te wyrażenia

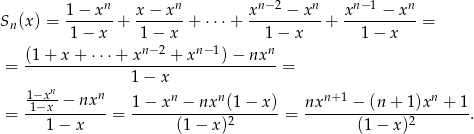
1− xn x − xn xn−2 − xn xn−1 − xn Sn(x) = -------+ -------+ ⋅⋅⋅+ ----------+ ----------= 1 − x 1− x 1− x 1− x (1-+-x-+-⋅⋅⋅+--xn−2-+-xn−-1)−--nxn- = 1− x = 1−xn- n n n n+1 n = -1−x-−-nx---= 1−--x-−--nx-(1-−-x-)= nx-----−-(n-+-1)x--+-1-. 1 − x (1− x)2 (1 − x )2

Sposób II

Zadanie można łatwo rozwiązać używając pochodnych. Mamy równość (wzór na sumę ciągu geometrycznego).

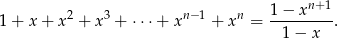
2 3 n−1 n 1− xn+1 1+ x+ x + x + ⋅⋅⋅+ x + x = -1-−-x---.

Zróżniczkujmy teraz tę równość stronami.

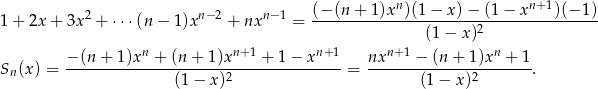
2 n−2 n−1 (− (n + 1 )xn)(1− x) − (1− xn+1)(− 1) 1+ 2x + 3x + ⋅⋅⋅(n − 1)x + nx = -----------------------2--------------- (1− x) −-(n-+-1)xn-+-(n-+-1)xn-+1 +-1−--xn+1- nxn-+1 −-(n-+-1)xn-+-1- Sn(x) = (1− x )2 = (1 − x)2 .

 
Odpowiedź: n+1 n Sn (x) = nx---−(n+1)2x-+1 (1−x)

Wersja PDF