/Szkoła średnia/Zadania maturalne/Matura 2009/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 28 marca 2009 Czas pracy: 120 minut
Dana jest funkcja liniowa 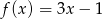 .
.
- Rozwiąż nierówność
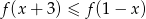 .
. - Podaj maksymalne przedziały monotoniczności funkcji
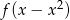 .
.
Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 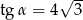 oblicz wartość wyrażenia
oblicz wartość wyrażenia 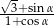 .
.
Napisz w postaci ogólnej, kanonicznej i iloczynowej wzór funkcji kwadratowej, jeśli do wykresu tej funkcji należy punkt 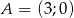 i funkcja osiąga wartość największą równą 12 dla argumentu 1.
i funkcja osiąga wartość największą równą 12 dla argumentu 1.
Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, których ostatnia cyfra jest równa 7.
Sprawdź czy punkt 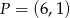 leży na dwusiecznej kąta
leży na dwusiecznej kąta 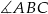 trójkąta o wierzchołkach
trójkąta o wierzchołkach 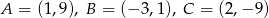 .
.
Dobierz wartości 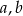 i
i  tak, aby liczby
tak, aby liczby 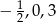 były pierwiastkami wielomianu
były pierwiastkami wielomianu 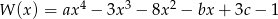 .
.
Pan Adam wpłacił na rachunek w funduszu inwestycyjnym pewną kwotę pieniędzy. Po roku stan rachunku zwiększył się o 4,5%, w drugim roku zmniejszył się o 5%, a w trzecim roku wzrósł o 4%. Wiedząc, że stan rachunku pana Adama po trzech latach oszczędzania wynosi 1548,69 zł oblicz jaką kwotę pan Adam początkowo wpłacił na ten rachunek.
Oblicz wartość wyrażenia 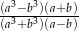 dla
dla 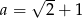 i
i 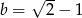 .
.
Z okrągłego skrawka materiału wycięto trójkąt równoboczny jak na rysunku poniżej.
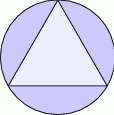
Oblicz jaki procent pola okrągłego skrawka stanowi pole wyciętego trójkąta. Przyjmując, że 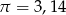 , wynik podaj z dokładnością do 1%.
, wynik podaj z dokładnością do 1%.
Ze zbioru liczb 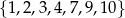 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.

