Oblicz z definicji pochodne jednostronne funkcji 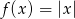 w punkcie
w punkcie 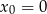 .
.
/Studia/Analiza/Funkcje
Oblicz granicę 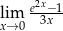 .
.
Oblicz granicę 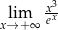 .
.
Oblicz granicę 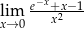 .
.
Oblicz granicę 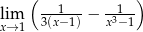 .
.
Oblicz granicę jednostronną funkcji 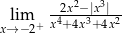 .
.
Oblicz wartość wyrażenia: 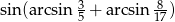 .
.
Oblicz wartość wyrażenia: 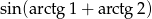 .
.
Wyznacz współrzędne punktu należącego do wykresu funkcji 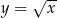 i takiego, że styczna do krzywej w tym punkcie jest nachylona do osi
i takiego, że styczna do krzywej w tym punkcie jest nachylona do osi 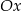 pod kątem
pod kątem 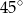 .
.
Naszkicuj wykres funkcji: 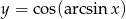 .
.
Oblicz granicę jednostronną
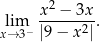
Oblicz granicę
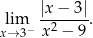
Oblicz granicę 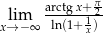 .
.
Funkcja 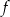 określona jest wzorem
określona jest wzorem 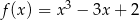 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 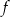 , które przechodzą przez punkt
, które przechodzą przez punkt 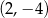 .
.
Napisz równanie stycznej do wykresu funkcji 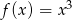 w punkcie
w punkcie 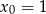 .
.
Dana jest parabola o równaniu 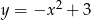 i leżący na niej punkt
i leżący na niej punkt 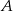 o współrzędnej
o współrzędnej  równej
równej 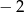 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 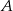 .
.
Dana jest parabola o równaniu 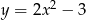 i leżący na niej punkt
i leżący na niej punkt 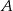 o współrzędnej
o współrzędnej  równej
równej 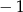 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 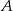 .
.
Napisz równanie stycznej do wykresu funkcji 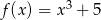 w punkcie
w punkcie 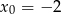 .
.
Dana jest parabola o równaniu 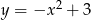 i leżący na niej punkt
i leżący na niej punkt 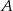 o współrzędnej
o współrzędnej  równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie 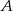 .
.
Napisz równanie stycznej do wykresu funkcji 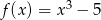 w punkcie
w punkcie 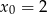 .
.
Dana jest parabola o równaniu 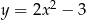 i leżący na niej punkt
i leżący na niej punkt 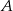 o współrzędnej
o współrzędnej  równej
równej 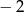 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 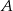 .
.
Dana jest parabola o równaniu 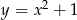 i leżący na niej punkt
i leżący na niej punkt 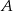 o współrzędnej
o współrzędnej  równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie 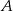 .
.
Dana jest parabola o równaniu 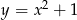 i leżący na niej punkt
i leżący na niej punkt 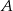 o współrzędnej
o współrzędnej  równej
równej 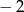 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 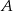 .
.
Dana jest parabola o równaniu 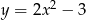 i leżący na niej punkt
i leżący na niej punkt 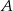 o współrzędnej
o współrzędnej  równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie 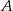 .
.
Napisz równanie stycznej do wykresu funkcji 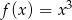 w punkcie
w punkcie 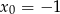 .
.
Dana jest parabola o równaniu 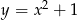 i leżący na niej punkt
i leżący na niej punkt 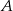 o współrzędnej
o współrzędnej  równej
równej 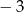 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 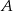 .
.
Dana jest parabola o równaniu 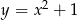 i leżący na niej punkt
i leżący na niej punkt 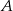 o współrzędnej
o współrzędnej  równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 2. Wyznacz równanie stycznej do tej paraboli w punkcie 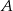 .
.
Dana jest parabola o równaniu 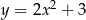 i leżący na niej punkt
i leżący na niej punkt 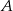 o współrzędnej
o współrzędnej  równej
równej 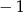 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 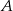 .
.
Dana jest parabola o równaniu 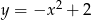 i leżący na niej punkt
i leżący na niej punkt 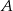 o współrzędnej
o współrzędnej  równej
równej 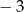 . Wyznacz równanie stycznej do tej paraboli w punkcie
. Wyznacz równanie stycznej do tej paraboli w punkcie 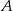 .
.
Napisz równanie stycznej do wykresu funkcji 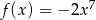 w punkcie
w punkcie 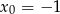 .
.
Dana jest parabola o równaniu 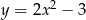 i leżący na niej punkt
i leżący na niej punkt 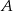 o współrzędnej
o współrzędnej  równej 1. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 1. Wyznacz równanie stycznej do tej paraboli w punkcie 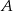 .
.
Dana jest parabola o równaniu 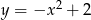 i leżący na niej punkt
i leżący na niej punkt 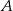 o współrzędnej
o współrzędnej  równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie
równej 3. Wyznacz równanie stycznej do tej paraboli w punkcie 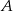 .
.
Oblicz pole trójkąta ograniczonego osią 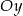 oraz stycznymi do wykresu funkcji
oraz stycznymi do wykresu funkcji 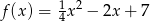 poprowadzonymi w punktach
poprowadzonymi w punktach 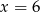 i
i 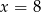 .
.
Funkcja 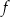 jest określona wzorem
jest określona wzorem 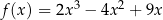 dla każdego
dla każdego 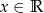 . Punkt
. Punkt 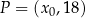 należy do wykresu funkcji
należy do wykresu funkcji 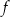 . Oblicz
. Oblicz 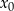 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 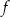 w punkcie
w punkcie 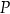 .
.
Funkcja 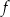 jest określona wzorem
jest określona wzorem 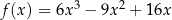 dla każdego
dla każdego 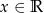 . Punkt
. Punkt 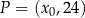 należy do wykresu funkcji
należy do wykresu funkcji 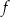 . Oblicz
. Oblicz 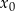 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 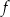 w punkcie
w punkcie 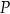 .
.
Oblicz pochodną funkcji 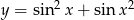 .
.
Oblicz pochodną funkcji 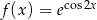 .
.
Oblicz granicę 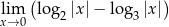 .
.
Oblicz z definicji pochodną funkcji stałej 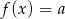 , gdzie
, gdzie 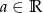 .
.
Oblicz z definicji pochodną funkcji kwadratowej 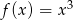 .
.
Oblicz z definicji pochodną funkcji liniowej 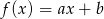 , gdzie
, gdzie 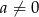 .
.
Oblicz z definicji pochodną funkcji liniowej 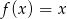 .
.
Oblicz z definicji pochodną funkcji kwadratowej 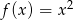 .
.
Funkcja 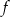 jest określona wzorem
jest określona wzorem 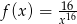 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 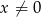 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 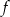 w punkcie
w punkcie 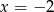 .
.
Oblicz odległość między stycznymi do wykresu funkcji 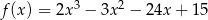 , które są równoległe do prostej
, które są równoległe do prostej 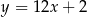 .
.
Uzasadnij, że nie istnieje granica 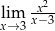 .
.

