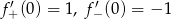Zadanie nr 8026012
Oblicz z definicji pochodne jednostronne funkcji 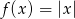 w punkcie
w punkcie 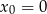 .
.
Rozwiązanie
Liczymy pochodną prawostronną
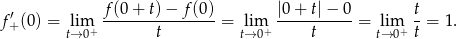
Teraz pochodna lewostronna.
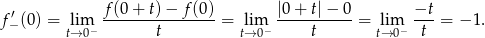
Odpowiedź: 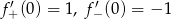
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz z definicji pochodne jednostronne funkcji 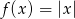 w punkcie
w punkcie 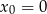 .
.
Liczymy pochodną prawostronną
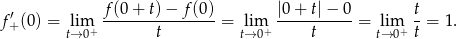
Teraz pochodna lewostronna.
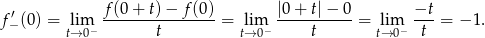
Odpowiedź: