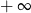Zadanie nr 8192638
Oblicz granicę jednostronną funkcji 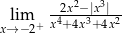 .
.
Rozwiązanie
Ponieważ
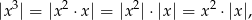
daną granicę możemy zapisać w postaci
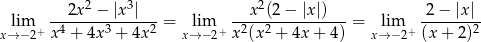
Teraz zauważmy, że 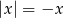 dla
dla 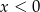 (a tak jest w naszym przypadku, bo
(a tak jest w naszym przypadku, bo 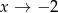 ). Powyższa granica jest więc równa
). Powyższa granica jest więc równa
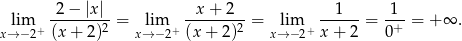
Odpowiedź: 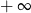
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę jednostronną funkcji 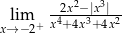 .
.
Ponieważ
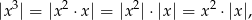
daną granicę możemy zapisać w postaci
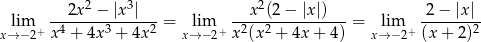
Teraz zauważmy, że 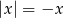 dla
dla 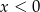 (a tak jest w naszym przypadku, bo
(a tak jest w naszym przypadku, bo 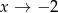 ). Powyższa granica jest więc równa
). Powyższa granica jest więc równa
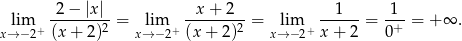
Odpowiedź: