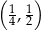/Studia/Analiza/Funkcje

Zadanie nr 8276843

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz współrzędne punktu należącego do wykresu funkcji 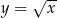√ -- y = x i takiego, że styczna do krzywej w tym punkcie jest nachylona do osi 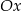Ox pod kątem 45∘ .

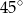Rozwiązanie

Musimy sprawdzić w jakich punktach pochodna danej funkcji jest równa 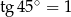tg 45∘ = 1 . Liczymy pochodną

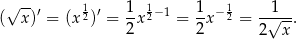
√ -- 1 1 1 ( x )′ = (x 2)′ = 1x 2−1 = 1x− 2 = -√1--. 2 2 2 x

Sprawdzamy w jakich punktach pochodna jest równa 1.

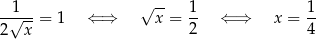
√ -- -√1-- = 1 ⇐ ⇒ x = 1- ⇐ ⇒ x = 1- 2 x 2 4

Jest więc jeden puhnkt spełniający warunki zadania: 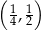( ) 14, 12 .

PIC

 
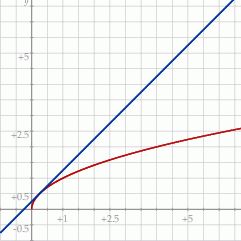
Odpowiedź: ( ) 14, 12

Wersja PDF