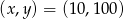/Szkoła średnia/Równania/Układy równań/Z logarytmami/Rozwiąż układ

Zadanie nr 6446497

Rozwiąż układ równań 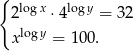{ logx logy 2 ⋅4 = 32 xlogy = 100.

Wersja PDF

Rozwiązanie

Przekształcamy podany układ równań

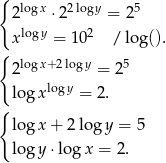
{ logx 2log y 5 2 ⋅2 = 2 x logy = 1 02 / lo g(). { 2logx+2 logy = 2 5 log xlogy = 2. { log x + 2log y = 5 log y⋅ lo gx = 2.

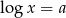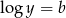Żeby nie męczyć się z przepisywaniem logarytmów, podstawmy logx = a i lo gy = b . Mamy wtedy

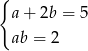
{ a+ 2b = 5 ab = 2

Podstawiamy 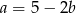a = 5− 2b do drugiego równania i mamy

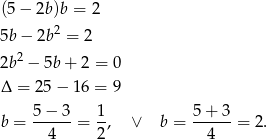
(5− 2b)b = 2 5b− 2b2 = 2 2b2 − 5b+ 2 = 0 Δ = 2 5− 16 = 9 5-−-3- 1- 5-+-3- b = 4 = 2, ∨ b = 4 = 2.

Wtedy odpowiednio

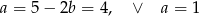
a = 5− 2b = 4, ∨ a = 1

Daje to nam

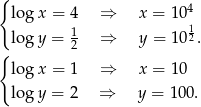
{ logx = 4 ⇒ x = 104 1 1 logy = 2 ⇒ y = 102. { logx = 1 ⇒ x = 10 logy = 2 ⇒ y = 100.

 
Odpowiedź: 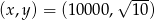√ --- (x,y ) = (10000, 1 0) lub (x,y ) = (10,100)

Wersja PDF