/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 5181704

Dodaj do ulubionych
Dodaj do rozwiązanych

Określić wymiar i wskazać przykładową bazę przestrzeni generowanej przez wektory:

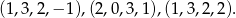
(1,3,2,− 1),(2,0,3,1),(1,3,2 ,2).

Rozwiązanie

Wstawimy wektory w macierz (pionowo) i policzymy jej rząd wykonując tylko operacje na kolumnach. Otrzymane na końcu wektory liniowo niezależne będą bazą podprzestrzeni generowanej przez te wektory.

Liczymy

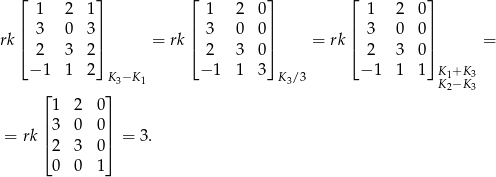
⌊ ⌋ ⌊ ⌋ ⌊ ⌋ 1 2 1 1 2 0 1 2 0 | 3 0 3| | 3 0 0| | 3 0 0| rk|⌈ |⌉ = rk |⌈ |⌉ = rk |⌈ |⌉ = 2 3 2 2 3 0 2 3 0 − 1 1 2 K3−K1 − 1 1 3 K3/3 − 1 1 1 KK1+−KK3 ⌊ ⌋ 2 3 1 2 0 ||3 0 0|| = rk ⌈2 3 0⌉ = 3. 0 0 1

Rząd jest 3, bo np. patrząc na 3 ostatnie wiersze widzimy, że są trzy wektory liniowo niezależne. Zatem kolumny też są liniowo niezależne i można je wziąć za bazę. Wymiar przestrzeni generowanej przez te wektory wynosi 3.  
Odpowiedź: Baza: (1,3,2,0),(2,0 ,3,0),(0,0,0,1)

Wersja PDF