/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 5386811

Dodaj do ulubionych
Dodaj do rozwiązanych

Znaleźć bazę przestrzeni wielomianów rzeczywistych co najwyżej 2-go stopnia spełniających warunek 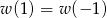w (1) = w (− 1) .

Rozwiązanie

Sprawdźmy, co podany warunek oznacza dla trójmianu 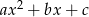2 ax + bx + c .

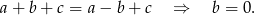
a + b + c = a − b + c ⇒ b = 0.

Zatem za bazę możemy wziąć układ

2 {1,x }

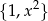
Jest jasne, że układ ten jest liniowo niezależny i generuje daną podprzestrzeń.  
Odpowiedź: {1 ,x 2}

Wersja PDF