/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 5578669

Dodaj do ulubionych
Dodaj do rozwiązanych

Określić wymiar i wskazać przykładową bazę przestrzeni generowanej przez wektory:

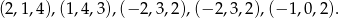
(2,1,4),(1,4,3),(− 2,3,2),(− 2,3,2 ),(− 1 ,0 ,2).

Rozwiązanie

Wstawimy wektory w macierz (pionowo) i policzymy jej rząd wykonując tylko operacje na kolumnach. Otrzymane na końcu wektory liniowo niezależne będą bazą podprzestrzeni generowanej przez te wektory.

Liczymy (od razu opuszczamy powtarzający się wektor).

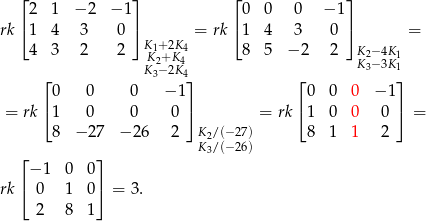
⌊ ⌋ ⌊ ⌋ 2 1 − 2 − 1 0 0 0 − 1 rk⌈ 1 4 3 0 ⌉ = rk⌈ 1 4 3 0 ⌉ = K1+ 2K4 4 3 2 2 K2+K4 8 5 − 2 2 KK23−−43KK11 ⌊ K3− 2K4⌋ ⌊ ⌋ 0 0 0 − 1 0 0 0 − 1 = rk⌈ 1 0 0 0 ⌉ = rk⌈ 1 0 0 0 ⌉ = 8 − 27 − 26 2 K /(−27) 8 1 1 2 K23/(−26) ⌊ ⌋ − 1 0 0 rk⌈ 0 1 0⌉ = 3. 2 8 1

Zatem wymiar jest równy 3 i za bazę możemy wziąć trzy powyższe wektory (kolumny).  
Odpowiedź: Baza: (− 1,0,2),(0,1,8 ),(0 ,0,1)

Wersja PDF