/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 6746746

Czy zbiór 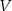V jest podprzestrzenią liniową przestrzeni 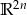2n R ? Jeśli tak to znaleźć jej bazę.

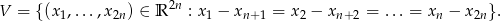
V = {(x1,...,x2n) ∈ R 2n : x1 − xn+1 = x2 − xn+2 = ... = xn − x 2n} .
Wersja PDF

Rozwiązanie

Przede wszystkim zauważmy, że podany warunek oznacza, że współrzędne 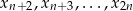xn+ 2,xn+3,...,x 2n są jednoznacznie wyznaczone przez współrzędne 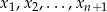x1,x 2,...,xn+1 . Rzeczywiście, jeżeli oznaczymy 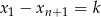x1 − xn+ 1 = k to

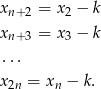
xn+ 2 = x2 − k x = x − k n+ 3 3 ... x2n = xn − k.

Współrzędne 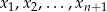x ,x ,...,x 1 2 n+ 1 są natomiast zupełnie dowolne.

Sposób I

Musimy się zastanowić, czy podany zbiór 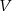V jest zamknięty ze względu sumę i mnożenie przez skalar. Aby nie mieć dwóch warunków, będziemy sprawdzać, czy

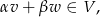
αv + βw ∈ V ,

gdzie 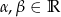α,β ∈ R i v,w ∈ V .

Jeżeli

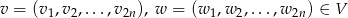
v = (v1,v2,...,v2n), w = (w 1,w 2,...,w 2n) ∈ V

to

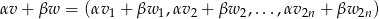
αv + βw = (αv 1 + βw 1,αv2 + βw 2,...,αv2n + βw 2n)

i wektor ten spełnia dany warunek, bo równość

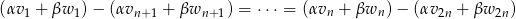
(αv1 + βw 1)− (αvn+1 + βwn + 1) = ⋅⋅⋅ = (αvn + βwn ) − (αv 2n + βw 2n)

możemy zapisać w postaci

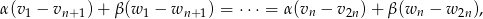
α(v1 − vn+ 1)+ β (w 1 − wn +1) = ⋅⋅⋅ = α(vn − v2n) + β(wn − w2n),

co oznacza, że jest ona konsekwencją założenia 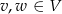v,w ∈ V .

Przy wyznaczaniu bazy będziemy korzystać z bazy standardowej:

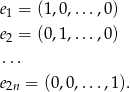
e = (1,0,...,0) 1 e2 = (0,1,...,0) ... e2n = (0,0,...,1).

Bazą tej podprzestrzeni jest układ (należy myśleć, że 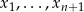x1,...,xn+ 1 są dowolne, a pozostałe współrzędne są wyznaczone z podanego warunku.)

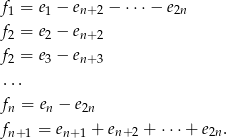
f = e − e − ⋅ ⋅⋅− e 1 1 n+ 2 2n f 2 = e2 − en+ 2 f = e − e 2 3 n+ 3 ... fn = en − e2n fn +1 = en+1 + en+ 2 + ⋅⋅⋅ + e2n.

Sprawdźmy, że układ ten jest liniowo niezależny

0 = α 1f1 + α 2f2 + ⋅ ⋅⋅+ αn+ 1fn+1 0 = α 1e1 + α 2e2 + ⋅⋅⋅ + αn+ 1en+ 1 + (∗),

gdzie (*) jest pewną kombinacją wektorów 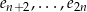e ,...,e n+ 2 2n – można ją dokładnie wyliczyć, ale nie ma ona znaczenia (ważne jest tylko, że nie ma tam wektorów 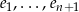e1,...,en+1 ). Z liniowej niezależności wektorów 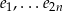e1,...e2n mamy

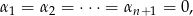
α1 = α2 = ⋅⋅⋅ = αn+1 = 0 ,

co dowodzi liniowej niezależności wektorów 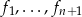f1,...,fn+ 1 . Pozostało sprawdzić, że generują one 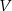V . Dla dowolnego

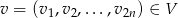
v = (v ,v2,...,v 2n) ∈ V 1

mamy

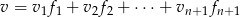
v = v1f1 + v2f2 + ⋅⋅⋅+ vn +1fn+ 1

(to wynika z tego, co już napisaliśmy: współrzędne 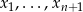x1,...,xn+ 1 jednoznacznie wyznaczają pozostałe).

Sposób II

Tym razem skorzystamy z faktu, że jądro odwzorowania liniowego jest podprzestrzenią liniową. W ten sposób łatwo możemy pokazywać, że zbiory wektorów tworzą podprzestrzenie.

Takie podejście ma jeszcze jedną zaletę, bo ze wzoru

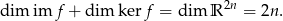
dim im f + d im kerf = dim R 2n = 2n .

będziemy wiedzieć jaki jest wymiar przestrzeni V . W wszystkich poniższych przykładach f będzie ’na’, więc

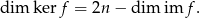
d im kerf = 2n − d im im f.

Dzięki temu znajdując bazę nie musimy sprawdzać, czy jej wektory są liniowo niezależne – wystarczy tylko, żeby generowały V i żeby była ich odpowiednia ilość.

Rozpatrzmy odwzorowanie liniowe

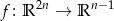
f : R 2n → Rn− 1

dane wzorem

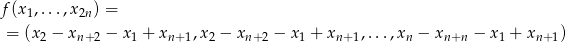
f(x1,...,x2n) = = (x2 − xn+ 2 − x 1 + xn +1,x2 − xn+ 2 − x 1 + xn +1,...,xn − xn+n − x1 + xn+1)

Jego jądro to dokładnie wektory spełniające warunek

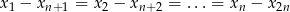
x1 − xn+ 1 = x2 − xn+ 2 = ...= xn − x2n

Bazę wyznaczamy jak w poprzednim sposobie, ale nie musimy już wykazywać jej liniowej niezależności.

Sposób III

Jeszcze inny sposób to skorzystanie z ogólnego faktu, że rozwiązania jednorodnego układu równań tworzą podprzestrzeń liniową. Używając tej metody można również wyznaczyć wektory bazowe jako rozwiązania podstawowe odpowiedniego układu równań.

Wersja PDF