/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 9777553

Dodaj do ulubionych
Dodaj do rozwiązanych

Czy zbiór 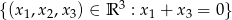3 {(x1,x2,x3) ∈ R : x1 + x3 = 0} jest podprzestrzenią linową R 3 ?

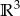Rozwiązanie

Musimy sprawdzić czy podany zbiór 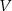V jest zamknięty ze względu na sumę wektorów:

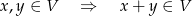
x,y ∈ V ⇒ x + y ∈ V

oraz na mnożenie przez skalar:

a ∈ R ,x ∈ V ⇒ ax ∈ V .

Niech

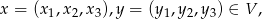
x = (x 1,x2,x3),y = (y1,y 2,y 3) ∈ V,

czyli

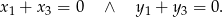
x1 + x3 = 0 ∧ y1 + y3 = 0.

Musimy sprawdzić czy tę samą własność mają wektory:

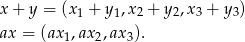
x + y = (x1 + y1,x2 + y2,x3 + y3) ax = (ax1,ax2,ax3).

To jednak jest jasne, bo

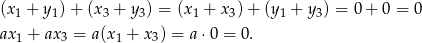
(x1 + y1) + (x3 + y3) = (x1 + x3) + (y1 + y3) = 0 + 0 = 0 ax1 + ax 3 = a(x1 + x3) = a ⋅0 = 0.

 
Odpowiedź: Tak, jest.

Wersja PDF