Zadanie nr 9363913
Czy zbiór 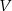 jest podprzestrzenią liniową przestrzeni
jest podprzestrzenią liniową przestrzeni 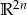 ? Jeśli tak to znaleźć jej bazę.
? Jeśli tak to znaleźć jej bazę.
Rozwiązanie
Musimy się zastanowić, czy podany zbiór 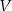 jest zamknięty ze względu sumę i mnożenie przez skalar. Aby nie mieć dwóch warunków, będziemy sprawdzać, czy
jest zamknięty ze względu sumę i mnożenie przez skalar. Aby nie mieć dwóch warunków, będziemy sprawdzać, czy
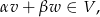
gdzie 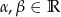 i
i 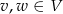 .
.
Jeżeli
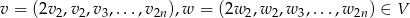
to
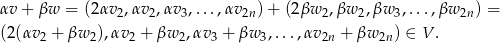
Przy wyznaczaniu bazy będziemy korzystać z bazy standardowej:
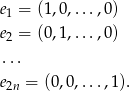
Bazą przestrzeni  jest układ wektorów
jest układ wektorów
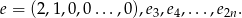
Łatwo sprawdzić, że jest on liniowo niezależny (bo 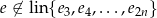 ), oraz dla dowolnego
), oraz dla dowolnego 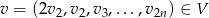 mamy
mamy
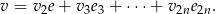
Sposób II
Tym razem skorzystamy z faktu, że jądro odwzorowania liniowego jest podprzestrzenią liniową. W ten sposób łatwo możemy pokazywać, że zbiory wektorów tworzą podprzestrzenie.
Takie podejście ma jeszcze jedną zaletę, bo ze wzoru
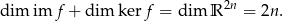
będziemy wiedzieć jaki jest wymiar przestrzeni 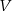 . W wszystkich poniższych przykładach
. W wszystkich poniższych przykładach 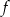 będzie ’na’, więc
będzie ’na’, więc
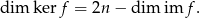
Dzięki temu znajdując bazę nie musimy sprawdzać, czy jej wektory są liniowo niezależne – wystarczy tylko, żeby generowały 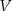 i żeby była ich odpowiednia ilość.
i żeby była ich odpowiednia ilość.
Rozpatrzmy odwzorowanie liniowe
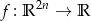
dane wzorem
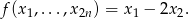
Jego jądro to dokładnie wektory spełniające warunek 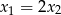 . Jest jasne, że to odwzorowanie jest ’na’, więc
. Jest jasne, że to odwzorowanie jest ’na’, więc
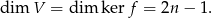
Bazę wyznaczamy jak poprzednio, ale nie musimy sprawdzać liniowej niezależności wektorów.
Sposób III
Jeszcze inny sposób to skorzystanie z ogólnego faktu, że rozwiązania jednorodnego układu równań tworzą podprzestrzeń liniową. Wszystkie podane podprzestrzenie są tego typu. Używając tej metody można również wyznaczyć wektory bazowe jako rozwiązania podstawowe odpowiedniego układu równań.

