Zadanie nr 1255784
Wykazać, że jeśli równanie liniowe 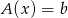 w
w 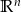 , ma dwa różne rozwiązania, to ma ich nieskończenie wiele.
, ma dwa różne rozwiązania, to ma ich nieskończenie wiele.
Rozwiązanie
Sposób I
Jeżeli 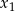 i
i 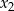 są dwoma różnymi rozwiązaniami, to
są dwoma różnymi rozwiązaniami, to
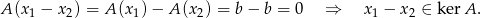
Ponieważ jądro jest podprzestrzenią liniową i jest niezerowe, więc jest nieskończone. Zatem każdy wektor postaci 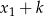 , gdzie
, gdzie 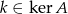 spełnia:
spełnia:
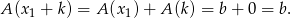
Sposób II
Jeżeli układ równań ma rozwiązania, to jest ich dokładnie tyle samo co rozwiązań odpowiadającego układu jednorodnego 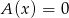 . Rozwiązania układu jednorodnego tworzą podprzestrzeń liniową i jeżeli zawiera ona dwa różne punkty to jest nieskończona.
. Rozwiązania układu jednorodnego tworzą podprzestrzeń liniową i jeżeli zawiera ona dwa różne punkty to jest nieskończona.
Sposób III
Jeżeli 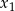 i
i 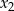 są dwoma różnymi rozwiązaniami równania
są dwoma różnymi rozwiązaniami równania 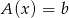 , to dla dowolnego
, to dla dowolnego 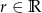 mamy
mamy
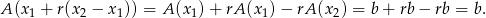
Zatem dowolny wektor postaci 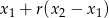 też jest rozwiązaniem układu.
też jest rozwiązaniem układu.

