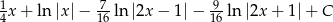/Studia/Analiza/Całki nieoznaczone/Wymierne

Zadanie nr 1911123

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 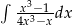∫ x3−1- 4x3−x dx .

Rozwiązanie

Najpierw zmniejszamy stopień licznika.

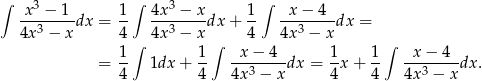
∫ 3 ∫ 3 ∫ x--−-1-dx = 1- 4x--−-xdx + 1- -x-−-4--dx = 4x3 − x 4 ∫ 4x3 − x ∫ 4 4x 3 − x ∫ 1- 1- -x−--4-- 1- 1- -x-−-4-- = 4 1dx + 4 4x3 − xdx = 4x + 4 4x 3 − x dx.

Pozostało obliczyć ostatnią całkę. Ponieważ

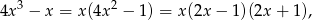
3 2 4x − x = x(4x − 1) = x(2x − 1)(2x + 1),

szukamy rozkładu funkcji podcałkowej na ułamki proste postaci

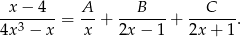
x− 4 A B C --------= --+ -------+ -------. 4x3 − x x 2x − 1 2x + 1

Mnożymy obie strony przez 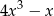3 4x − x i mamy

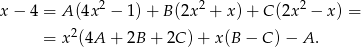
2 2 2 x − 4 = A(4x − 1)+ B (2x + x) + C (2x − x) = = x2(4A + 2B + 2C )+ x(B − C )− A .

Otrzymujemy stąd układ

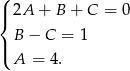
( |{ 2A + B + C = 0 B − C = 1 |( A = 4.

Łatwo stąd wyliczyć: 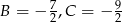7 9 B = − 2,C = − 2 . Zatem

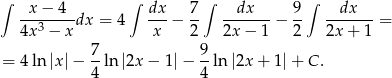
∫ x − 4 ∫ dx 7 ∫ dx 9 ∫ dx --3-----dx = 4 ---− -- -------− -- -------= 4x − x x 2 2x − 1 2 2x + 1 7- 9- = 4 ln |x|− 4 ln |2x− 1|− 4 ln |2x+ 1|+ C .

Wracamy do wyjściowej całki.

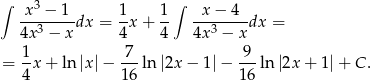
∫ ∫ x3-−-1-- 1- 1- -x-−-4-- 4x3 − xdx = 4x + 4 4x 3 − x dx = 1 7 9 = -x + ln |x |− ---ln |2x − 1|− ---ln |2x + 1|+ C . 4 1 6 1 6

 
Odpowiedź: 1 7 9 4x + ln |x |− 16 ln |2x − 1|− 16 ln |2x + 1|+ C

Wersja PDF