/Studia/Analiza/Całki nieoznaczone/Trygonometryczne

Zadanie nr 2414464

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 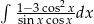∫ 1−3cos2x sinx cosx dx .

Rozwiązanie

Sposób I

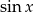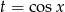Mnożymy licznik i mianownik wyrażenia podcałkowego przez sin x tak, aby móc podstawić t = co sx .

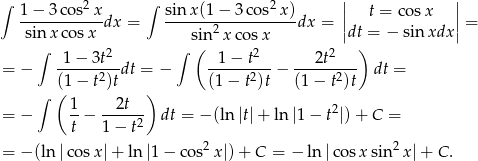
∫ 2 ∫ 2 | | 1-−-3-cos-x-dx = sinx-(1−--3cos--x)dx = || t = cosx ||= sinx cosx sin 2xc osx |dt = − sin xdx | ∫ 2 ∫ ( 2 2 ) = − -1-−-3t--dt = − -1-−-t---− --2t----- dt = (1 − t2)t (1− t2)t (1− t2)t ∫ ( 1 2t ) = − --− -----2 dt = − (ln |t| + ln|1 − t2|) + C = t 1 − t = − (ln| cosx| + ln|1 − cos2 x|)+ C = − ln |cosx sin2x |+ C .

Sposób II

Korzystamy z jedynki trygonometrycznej

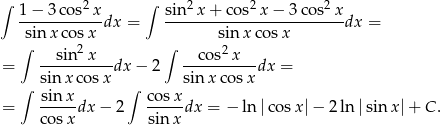
∫ 1− 3cos2 x ∫ sin 2x + cos2 x− 3cos2 x -----------dx = ------------------------dx = sin xco sx sin x cosx ∫ sin 2x ∫ cos2 x = ----------dx − 2 ----------dx = ∫ sin x cosx ∫ sinx cos x = sin-x-dx − 2 cos-xdx = − ln |cosx |− 2 ln |sinx |+ C . cosx sin x

Ostatnie dwie całki policzyliśmy w pamięci, ale równie dobrze można było podstawić 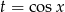t = co sx w pierwszej i 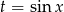t = sinx w drugiej.  
Odpowiedź: 2 − ln| cosx sin x|+ C

Wersja PDF