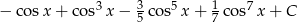Zadanie nr 9985046
Oblicz całkę 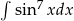 .
.
Rozwiązanie
Będziemy dążyć (używając jedynki trygonometrycznej) do postawienia 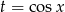 .
.
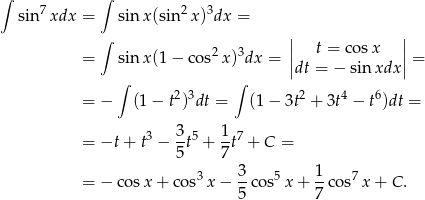
Odpowiedź: 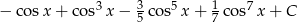
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 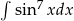 .
.
Będziemy dążyć (używając jedynki trygonometrycznej) do postawienia 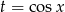 .
.
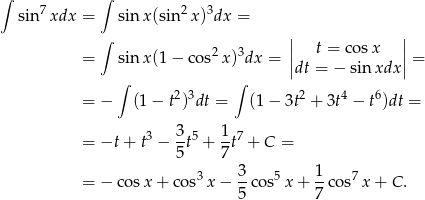
Odpowiedź: