Zadanie nr 6631948
Rzucamy trzy razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 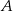 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
Rozwiązanie
Przyjmijmy, że zdarzenia elementarne to uporządkowane trójki wylosowanych liczb. Zatem
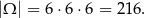
W zdarzeniach przeciwnych do zdarzenia opisanego w treści zadania na żadnej z kostek nie ma dwójki. Zatem
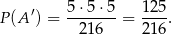
Stąd
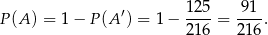
Odpowiedź: