/Szkoła podstawowa/Geometria/Trójkąt/Równoramienny

Zadanie nr 1604874

W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 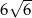√ -- 6 6 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.

Wersja PDF

Rozwiązanie

Zacznijmy od rysunku

PIC

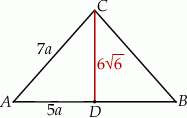
Oznaczyliśmy długość podstawy przez 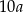10a , dzięki temu nie będziemy mieli ułamków. Ramię ma długość 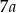7a i z stosując twierdzenie Pitagorasa w trójkącie 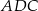ADC mamy

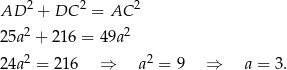
AD 2 + DC 2 = AC 2 2 2 25a + 21 6 = 49a 24a 2 = 216 ⇒ a2 = 9 ⇒ a = 3.

Zatem obwód jest równy

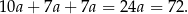
10a + 7a + 7a = 24a = 72.

 
Odpowiedź: 72

Wersja PDF