/Szkoła podstawowa/Geometria/Trójkąt/Równoramienny

Zadanie nr 2773350

Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

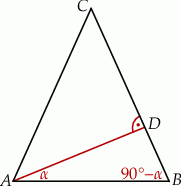
Trójkąt 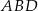ABD jest prostokątny, więc jeżeli oznaczymy 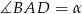∡BAD = α , to

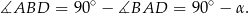
∡ABD = 90∘ − ∡BAD = 90∘ − α .

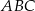Trójkąt ABC jest równoramienny, więc

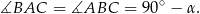
∡BAC = ∡ABC = 90∘ − α.

Mamy zatem

∡ACB = 180∘ − ∡BAC − ∡ABC = 1 80∘ − 2⋅(9 0∘ − α ) = 2α.
Wersja PDF