/Szkoła podstawowa/Geometria/Trójkąt/Równoramienny

Zadanie nr 3503552

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt ostrokątny równoramienny 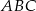ABC , w którym bok 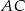AC jest równy 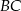BC . Odcinek 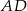AD jest wysokością tego trójkąta, oraz odcinek 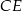CE jest wysokością tego trójkąta. Udowodnij, że kąt 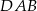DAB jest równy kątowi ECB .

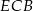Rozwiązanie

Oznaczmy 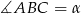∡ABC = α .

PIC

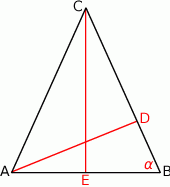
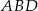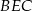Ponieważ każdy z trójkątów ABD i BEC jest prostokątny, mamy

∡DAB = 90 ∘ − α = ∡ECB .
Wersja PDF