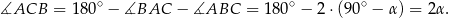Zadanie nr 9519144
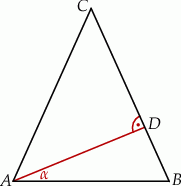
Odcinek 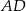 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 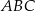 , w którym
, w którym 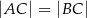 . Udowodnij, że
. Udowodnij, że 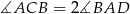 .
.
Rozwiązanie
Oznaczmy 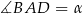 .
.
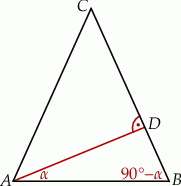
Trójkąt 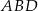 jest prostokątny, więc
jest prostokątny, więc
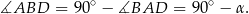
Trójkąt 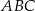 jest równoramienny, więc
jest równoramienny, więc
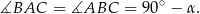
Mamy zatem
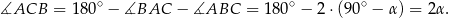
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odcinek 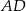 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 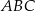 , w którym
, w którym 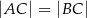 . Udowodnij, że
. Udowodnij, że 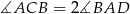 .
.

Oznaczmy 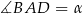 .
.

Trójkąt 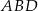 jest prostokątny, więc
jest prostokątny, więc
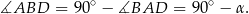
Trójkąt 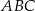 jest równoramienny, więc
jest równoramienny, więc
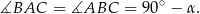
Mamy zatem