Zadanie nr 3681280

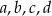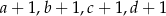Odchylenie standardowe liczb: a,b,c,d jest równe 0,1. Oblicz odchylenie standardowe danych: a+ 1,b+ 1,c+ 1 ,d+ 1 .

Rozwiązanie

Jeżeli oznaczymy przez

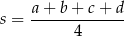
a+ b+ c + d s = ------------- 4

średnią arytmetyczną pierwszych 4 liczb, to wiemy, że

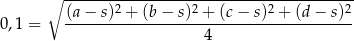
∘ -------2----------2---------2----------2 0,1 = (a−--s)--+-(b-−-s)-+--(c−--s)--+-(d-−-s)-- 4

Liczymy teraz średnią arytmetyczną kolejnych czterech liczb

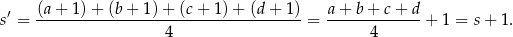
(a+ 1)+ (b + 1) + (c + 1) + (d + 1) a+ b+ c + d s′ = -------------------------------------= -------------+ 1 = s+ 1. 4 4

Interesujące nas odchylenie standardowe jest więc równe

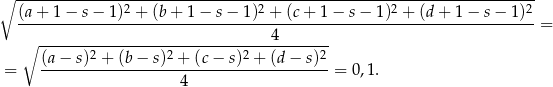
∘ ------------------------------------------------------------------------ (a-+-1-−-s-−-1)2 +-(b+--1−--s−-1-)2 +-(c-+-1-−-s−-1)2 +-(d+--1−--s−-1)2 4 = ∘ ---------------------------------------- (a−-s)2-+-(b-−-s)2 +-(c−-s)2-+-(d-−-s)2- = 4 = 0 ,1.

Odpowiedź: 0,1