Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Promień okręgu opisanego na tym trójkącie jest równy
A) 12 B) 8,5 C) 6,5 D) 5
/Szkoła średnia/Zadania testowe
Na trójkącie prostokątnym, którego przyprostokątne mają długości 12 i 9, opisano okrąg. Promień tego okręgu jest równy
A) 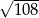 B)
B) 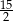 C) 15 D)
C) 15 D) 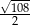
Promień kuli jest równy promieniowi podstawy walca, oraz objętości obu brył są równe. Stosunek pola powierzchni kuli do pola powierzchni całkowitej walca jest równy
A) 1 B)  C)
C) 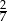 D)
D) 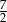
Dla jakiej wartości parametru 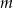 punkt przecięcia prostych
punkt przecięcia prostych 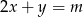 i
i 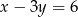 należy do osi
należy do osi 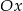 ?
?
A) dla 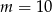 B) dla
B) dla 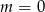 C) dla
C) dla 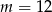 D) dla
D) dla 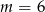
Proste o równaniach 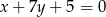 i
i 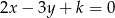 przecinają się na osi
przecinają się na osi 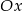 . Zatem parametr
. Zatem parametr 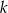 jest równy
jest równy
A) 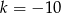 B)
B) 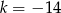 C)
C) 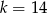 D)
D) 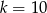
W trójkącie prostokątnym o polu 15 najkrótszy bok ma długość 3. Obwód tego trójkąta jest równy
A) 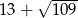 B)
B) 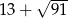 C)
C) 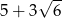 D)
D) 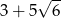
Środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
A) dwusiecznych kątów trójkąta B) środkowych trójkąta
C) wysokości trójkąta D) symetralnych boków trójkąta
Dla dowolnego trójkąta prawdziwe jest zdanie
A) Środek okręgu wpisanego w trójkąt to punkt przecięcia się środkowych trójkąta.
B) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się dwusiecznych kątów trójkąta.
D) Środek okręgu opisanego na trójkącie to punkt przecięcia się wysokości trójkąta
Dany jest ciąg o wyrazie ogólnym 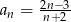 . Wynika stąd, że
. Wynika stąd, że
A) 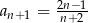 B)
B) 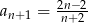 C)
C) 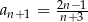 D)
D) 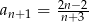
Dany jest ciąg o wyrazie ogólnym 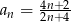 . Wynika stąd, że
. Wynika stąd, że
A) 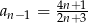 B)
B) 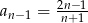 C)
C) 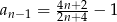 D)
D) 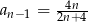
Dany jest stożek o objętości 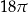 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 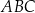 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 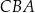 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 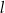 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 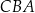 jest równy 2.
jest równy 2.
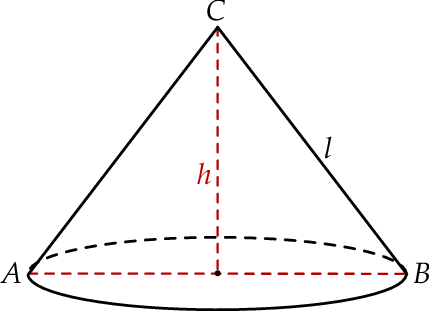
Wynika stąd, że wysokość 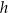 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Obrazem odcinka 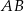 o końcach w punktach
o końcach w punktach 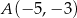 ,
, 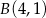 w symetrii względem osi
w symetrii względem osi 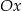 , jest odcinek
, jest odcinek 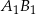 o końcach w punktach
o końcach w punktach
A) 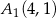 ,
, 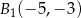 B)
B) 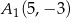 ,
, 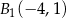
C) 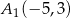 ,
, 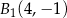 D)
D) 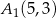 ,
, 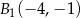
Przekątna kwadratu jest o 2 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 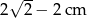 B)
B) 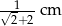 C)
C) 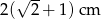 D)
D) 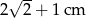
Przekątna kwadratu jest o 3 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 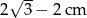 B)
B) 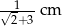 C)
C) 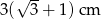 D)
D) 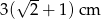
Przekątna kwadratu jest o 4 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 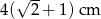 B)
B) 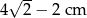 C)
C) 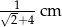 D)
D) 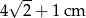
Wartość wyrażenia 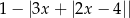 , dla
, dla 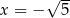 jest równa
jest równa
A) 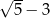 B)
B) 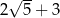 C)
C) 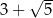 D)
D) 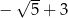
Wartość wyrażenia 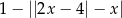 , dla
, dla 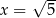 jest równa
jest równa
A) 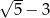 B)
B) 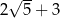 C)
C) 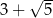 D)
D) 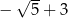
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 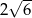 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 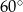 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 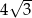 B) 6 C) 12 D) 4
B) 6 C) 12 D) 4
Przekątna graniastosłupa prawidłowego czworokątnego o długości równej 10 cm jest nachylona do płaszczyzny podstawy pod kątem 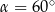 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 5 cm B) 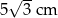 C)
C) 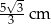 D)
D) 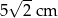
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36, a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 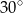 . Wysokość tego graniastosłupa jest równa
. Wysokość tego graniastosłupa jest równa
A) 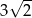 B)
B) 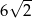 C)
C) 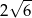 D)
D) 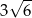
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 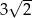 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 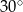 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 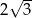 B) 6 C)
B) 6 C) 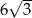 D) 4
D) 4
Przekątna graniastosłupa prawidłowego czworokątnego ma długość równą 16 i jest nachylona do płaszczyzny podstawy pod kątem 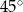 . Wysokość tego graniastosłupa ma długość równą
. Wysokość tego graniastosłupa ma długość równą
A) 8 B) 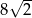 C)
C) 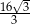 D)
D) 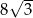
Ciąg 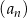 jest określony wzorem
jest określony wzorem 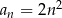 dla
dla 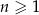 . Różnica
. Różnica 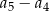 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
Ciąg 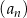 jest określony wzorem
jest określony wzorem 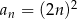 dla
dla 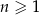 . Różnica
. Różnica 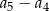 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
Funkcja 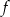 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji
ostatnią cyfrę jej kwadratu. Zbiór wartości funkcji 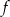 zawiera dokładnie
zawiera dokładnie
A) 5 elementów. B) 6 elementów. C) 9 elementów. D) 10 elementów.
Funkcja 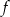 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  ostatnią cyfrę jej sześcianu. Zbiór wartości funkcji
ostatnią cyfrę jej sześcianu. Zbiór wartości funkcji 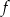 zawiera dokładnie
zawiera dokładnie
A) 5 elementów. B) 6 elementów. C) 9 elementów. D) 10 elementów.
Dany jest trójkąt prostokątny o kątach ostrych  i
i 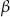 , w którym
, w którym 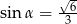 . Wtedy
. Wtedy
A) 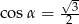 B)
B) 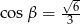 C)
C) 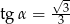 D)
D) 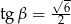
Liczba 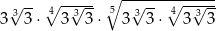 jest równa
jest równa
A) 9 B) 3 C) 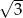 D)
D) 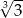
Suma rozwiązań równania 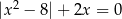 jest równa
jest równa
A) 0 B) 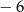 C) 2 D)
C) 2 D) 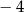
Rzucamy trzy razy symetryczną monetą. Niech 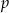 oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A) 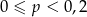 B)
B) 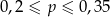 C)
C) 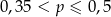 D)
D) 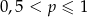
Rzucamy trzy razy symetryczną monetą. Niech 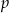 oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
A) 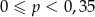 B)
B) 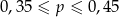 C)
C) 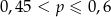 D)
D) 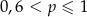
Rzucamy trzy razy symetryczną monetą. Niech 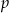 oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
A) 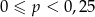 B)
B) 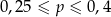 C)
C) 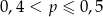 D)
D) 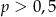
Kartkę papieru przecinamy na pół. Następnie jedną z otrzymanych części znowu przecinamy na pół i tak postępujemy dalej, aż uzyskamy w sumie 100 części. Liczba cięć które należy wykonać, jest równa
A) 100 B) 99 C) 50 D) 49
Kartkę papieru przecinamy na pół. Następnie jedną z otrzymanych części znowu przecinamy na pół i tak postępujemy dalej, aż uzyskamy w sumie 50 części. Liczba cięć które należy wykonać, jest równa
A) 50 B) 51 C) 49 D) 25
Patyk łamiemy na pół. Następnie jedną z otrzymanych części znowu łamiemy na pół, i postępujemy tak dalej, aż uzyskamy w sumie 30 części. Liczba łamań, które należy wykonać, jest równa
A) 29 B) 30 C) 31 D) 60
Za wykopanie pierwszego metra studni zapłacono 75 złotych. Wykopanie każdego następnego metra kosztowało dwa razy tyle co poprzedniego. Za wykopanie studni zapłacono 76725 złotych. Głębokość studni wynosiła
A) 7 m B) 8 m C) 9 m D) 10 m
Piotrek przygotowywał się do przeprowadzki i miał zamiar przygotować wszystko w ciągu  godzin. Kasia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje
godzin. Kasia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Piotrka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Piotrka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
A) 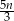 godzin B)
godzin B) 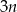 godzin C)
godzin C) 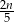 godzin D)
godzin D) 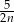 godzin
godzin
Janek przygotowywał się do przeprowadzki i miał zamiar przygotować wszystko w ciągu  godzin. Małgosia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje
godzin. Małgosia i Ania postanowiły mu pomóc, przy czym każda z dziewczynek w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Janka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Janka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
A) 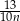 godzin B)
godzin B) 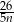 godzin C)
godzin C) 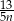 godzin D)
godzin D) 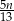 godzin
godzin
Wojtek przygotowywał się do przeprowadzki i miał zamiar przygotować wszystko w ciągu  godzin. Zosia i Ela postanowiły mu pomóc, przy czym każda z pań w ciągu jednej godziny wykonuje
godzin. Zosia i Ela postanowiły mu pomóc, przy czym każda z pań w ciągu jednej godziny wykonuje  pracy wykonanej w tym czasie przez Wojtka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
pracy wykonanej w tym czasie przez Wojtka. Zatem wszystkie trzy osoby, pracując razem, ukończą pracę w ciągu
A) 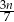 godzin B)
godzin B) 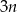 godzin C)
godzin C) 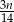 godzin D)
godzin D) 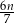 godzin
godzin
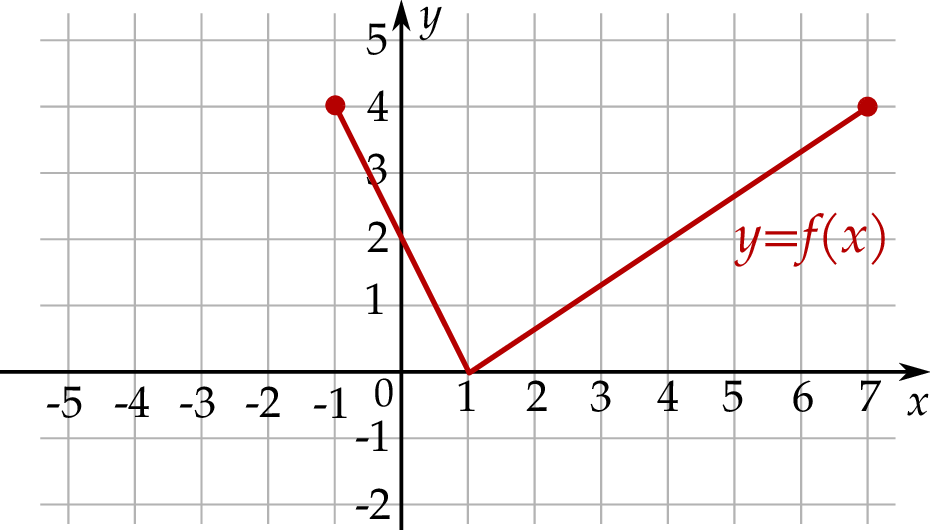
Na rysunku, w kartezjańskim układzie współrzędnych 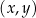 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 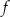 . Każdy z punktów przecięcia wykresu funkcji
. Każdy z punktów przecięcia wykresu funkcji 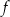 z prostą o równaniu
z prostą o równaniu 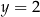 ma obie współrzędne całkowite.
ma obie współrzędne całkowite.
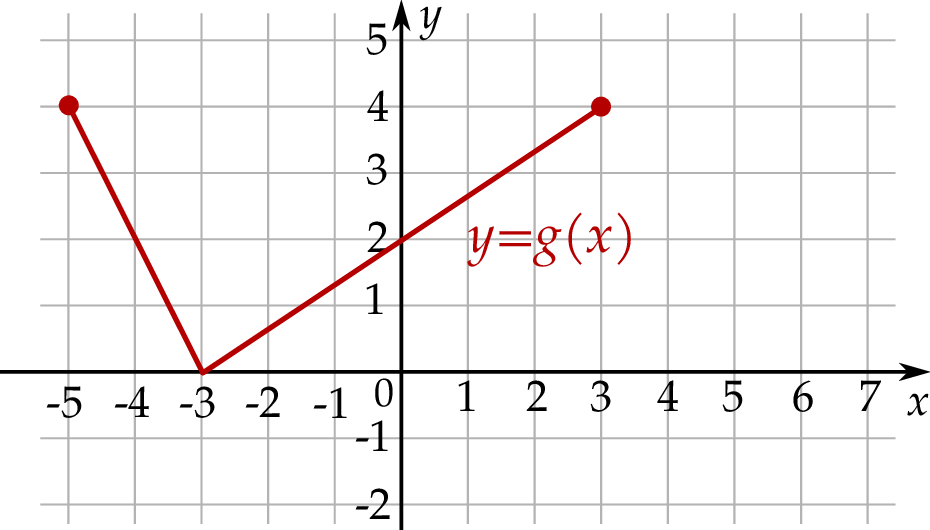
Na kolejnym rysunku przedstawiono wykres funkcji 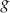 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 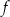 wzdłuż osi
wzdłuż osi 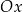 o 4 jednostki w lewo.
o 4 jednostki w lewo.
Funkcje 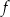 i
i 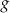 są powiązane zależnością
są powiązane zależnością
A) 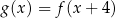 , , | B) 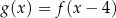 , , | C) 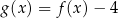 , , |
oraz mają takie same
| 1) dziedziny. | 2) zbiory wartości. |

