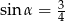Okresem podstawowym funkcji 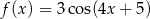 określonej dla
określonej dla 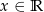 jest liczba
jest liczba
A) 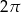 B)
B) 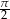 C)
C) 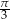 D)
D) 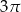
/Szkoła średnia/Zadania testowe
Funkcja 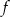 przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego
przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego 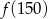 jest równe:
jest równe:
A) 11 B) 12 C) 13 D) 10
Funkcja 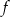 przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego
przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego 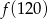 jest równe:
jest równe:
A) 8 B) 12 C) 32 D) 16
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
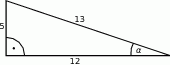
A) 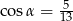 B)
B) 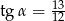 C)
C) 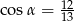 D)
D) 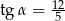
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
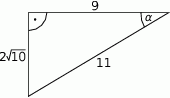
A) 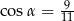 B)
B) 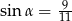 C)
C) 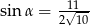 D)
D) 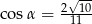
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
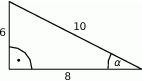
A) 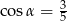 B)
B) 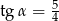 C)
C) 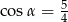 D)
D) 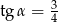
Jeżeli punkty 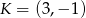 i
i 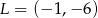 są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
A) 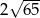 B)
B) 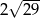 C)
C) 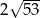 D)
D) 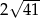
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 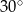 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 32 B) 16 C) 12 D) 8
Przekątne równoległoboku mają długości 4 i 8, a kąt między tymi przekątnymi ma miarę 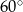 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 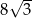 B)
B) 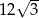 C)
C) 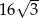 D)
D) 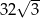
Dane są wielomiany 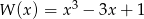 oraz
oraz 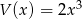 . Wielomian
. Wielomian 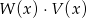 jest równy
jest równy
A) 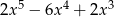 B)
B) 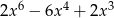 C)
C) 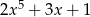 D)
D) 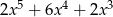
Iloczyn wielomianów 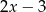 oraz
oraz 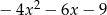 jest równy
jest równy
A) 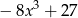 B)
B) 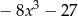 C)
C) 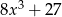 D)
D) 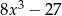
Dane są wielomiany 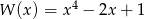 oraz
oraz 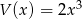 . Wielomian
. Wielomian 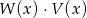 jest równy
jest równy
A) 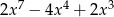 B)
B) 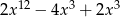 C)
C) 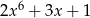 D)
D) 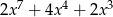
Dane są wielomiany 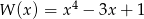 oraz
oraz 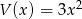 . Wielomian
. Wielomian 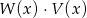 jest równy
jest równy
A) 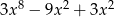 B)
B) 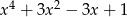 C)
C) 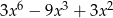 D)
D) 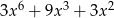
Dane są wielomiany 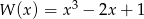 oraz
oraz 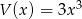 . Wielomian
. Wielomian 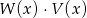 jest równy
jest równy
A) 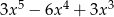 B)
B) 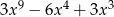 C)
C) 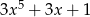 D)
D) 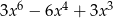
Iloczyn wielomianów 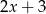 oraz
oraz 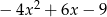 jest równy
jest równy
A) 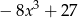 B)
B) 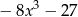 C)
C) 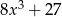 D)
D) 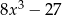
Punkty 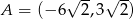 i
i 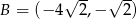 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 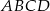 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 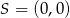 . Środek boku
. Środek boku 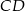 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 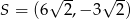 B)
B) 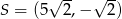 C)
C) 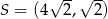 D)
D) 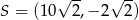
Zbiorem wartości funkcji 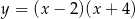 jest przedział
jest przedział
A) 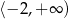 B)
B) 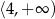 C)
C) 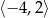 D)
D) 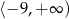
Zbiorem wartości funkcji 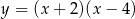 jest przedział
jest przedział
A) 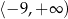 B)
B) 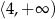 C)
C) 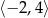 D)
D) 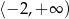
Zbiorem rozwiązań nierówności 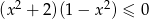 jest
jest
A) 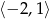 B)
B) 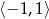 C)
C) 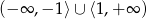 D)
D) 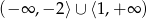
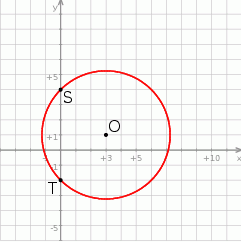
Okrąg przedstawiony na rysunku ma środek w punkcie 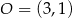 i przechodzi przez punkty
i przechodzi przez punkty 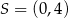 i
i  . Okrąg ten jest opisany przez równanie
. Okrąg ten jest opisany przez równanie
A) 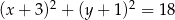 B)
B) 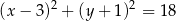
C) 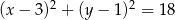 D)
D) 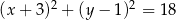
Zbiór rozwiązań nierówności kwadratowej 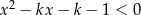 z niewiadomą
z niewiadomą  i parametrem
i parametrem 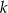 , jest taki sam jak zbiór rozwiązań nierówności
, jest taki sam jak zbiór rozwiązań nierówności 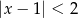 . Liczba
. Liczba 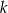 jest równa
jest równa
A) 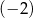 B) 2 C)
B) 2 C) 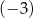 D) 3
D) 3
Liczba 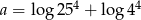 . Wynika stąd, że
. Wynika stąd, że
A) 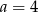 B)
B) 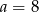 C)
C) 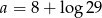 D)
D) 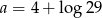
Liczba 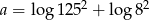 . Wynika stąd, że
. Wynika stąd, że
A) 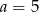 B)
B) 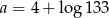 C)
C) 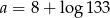 D)
D) 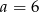
Liczba 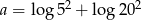 . Wynika stąd, że
. Wynika stąd, że
A) 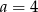 B)
B) 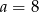 C)
C) 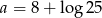 D)
D) 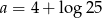
Wiadomo, że 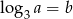 . Wtedy
. Wtedy 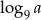 równa się
równa się
A) 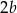 B)
B)  C)
C) 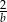 D)
D) 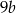
Wiadomo, że 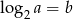 . Wtedy
. Wtedy 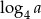 równa się
równa się
A) 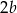 B)
B) 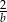 C)
C)  D)
D) 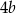
Wiadomo, że 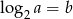 . Wtedy
. Wtedy 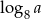 równa się
równa się
A) 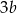 B)
B) 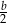 C)
C) 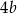 D)
D) 
W grupie 320 respondentów przeprowadzono ankietę, w której zapytano o liczbę wysłanych przez nich wiadomości e-mail pomiędzy 1 a 6 marca. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba e-maili | 10 | 20 | 30 | 40 | 50 | 60 |
| Liczba osób | 53 | 93 | 28 | 75 | 44 | 27 |
A) 5 B) 10 C) 4 D) 6
Która z liczb jest największa?
A) 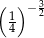 B)
B) 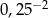 C)
C) 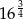 D)
D) 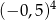
Liczbą większą od 3 jest
A) 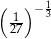 B)
B) 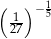 C)
C) 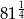 D)
D) 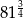
Która z liczb jest największa?
A) 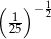 B)
B) 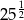 C)
C) 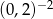 D)
D) 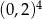
Liczbą mniejszą od 3 jest
A) 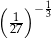 B)
B) 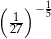 C)
C) 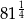 D)
D) 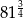
Liczbą większą od 5 jest
A) 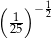 B)
B) 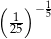 C)
C) 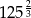 D)
D) 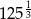
Iloraz liczb 5670 i 6615 jest równy
A) 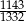 B)
B) 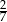 C)
C)  D)
D) 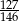
Iloraz liczb 2016 i 4704 jest równy
A) 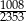 B)
B) 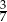 C)
C)  D)
D) 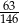
W graniastosłupie prawidłowym sześciokątnym 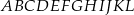 wierzchołki
wierzchołki 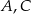 i
i 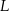 połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
połączono odcinkami (tak jak na rysunku). Wszystkie krawędzie graniastosłupa mają tą samą długość.
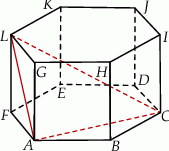
Cosinus największego kąta trójkąta 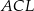 jest równy
jest równy
A)  B)
B) 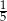 C) 0 D)
C) 0 D) 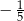
Rysunek przedstawia wykresy funkcji 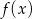 i
i 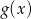 .
.
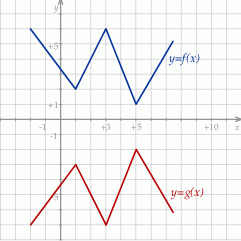
Prawdziwa jest równość:
A) 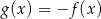 B)
B) 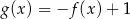 C)
C) 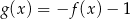 D)
D) 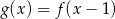
Rysunek przedstawia wykresy funkcji 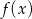 i
i 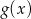 .
.
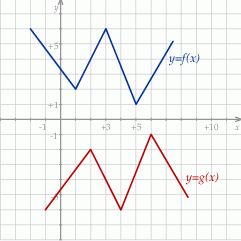
Prawdziwa jest równość:
A) 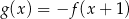 B)
B) 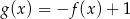
C) 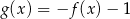 D)
D) 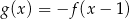
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 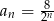 , gdzie
, gdzie 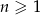 jest równy
jest równy
A) 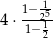 B)
B) 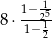 C)
C) 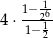 D)
D) 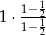
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 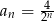 , gdzie
, gdzie 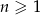 jest równy
jest równy
A) 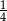 B)
B) 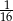 C)
C) 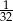 D)
D) 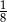
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 3:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 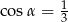 B)
B) 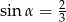 C)
C) 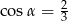 D)
D) 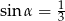
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 5:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 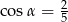 B)
B) 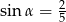 C)
C) 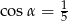 D)
D) 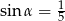
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 8:6. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 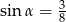 B)
B) 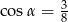 C)
C) 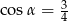 D)
D)