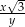Punkty 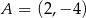 i
i 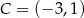 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 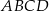 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 50 B) 100 C) 25 D) 12,5
/Szkoła średnia/Zadania testowe
W kartezjańskim układzie współrzędnych 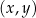 punkty
punkty 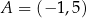 oraz
oraz 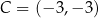 są wierzchołkami kwadratu
są wierzchołkami kwadratu 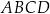 . Pole kwadratu
. Pole kwadratu 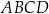 jest równe
jest równe
A) 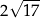 B)
B) 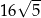 C) 68 D) 34
C) 68 D) 34
Punkty 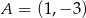 i
i 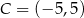 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 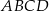 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
Punkty 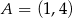 i
i 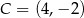 wyznaczają przekątną kwadratu
wyznaczają przekątną kwadratu  . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 45 B) 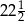 C) 18 D)
C) 18 D) 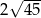
Punkty 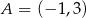 i
i 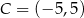 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 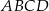 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
Punkty 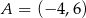 i
i 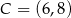 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 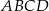 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 4 B) 52 C) 104 D) 26
W kartezjańskim układzie współrzędnych 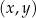 punkty
punkty 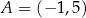 oraz
oraz 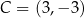 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 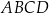 . Pole kwadratu
. Pole kwadratu 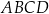 jest równe
jest równe
A) 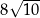 B)
B) 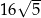 C) 40 D) 80
C) 40 D) 80
Punkty 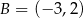 i
i 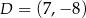 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 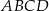 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 50 B) 100 C) 25 D) 200
Suma ciągu arytmetycznego jest określona wzorem 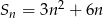 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 24 B) 15 C) 6 D) 2
Suma częściowa ciągu arytmetycznego jest wyrażona wzorem 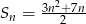 . Wobec tego:
. Wobec tego:
A) 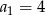 B)
B) 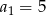 C)
C) 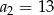 D)
D) 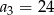
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 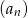 jest określona wzorem
jest określona wzorem 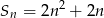 . Wtedy wyraz
. Wtedy wyraz 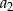 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Jeżeli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 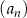 określona jest wzorem
określona jest wzorem 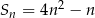 , to wartość piątego wyrazu tego ciągu jest równa
, to wartość piątego wyrazu tego ciągu jest równa
A) 33 B) 35 C) 60 D) 95
Suma ciągu arytmetycznego jest określona wzorem 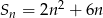 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 20 B) 16 C) 12 D) 8
Jeśli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 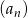 określona jest wzorem
określona jest wzorem 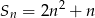 , to wartość trzeciego wyrazu tego ciągu jest równa
, to wartość trzeciego wyrazu tego ciągu jest równa
A) 8 B) 10 C) 11 D) 21
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 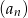 jest określona wzorem
jest określona wzorem 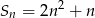 . Wtedy wyraz
. Wtedy wyraz 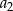 jest równy
jest równy
A) 3 B) 6 C) 7 D) 10
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 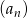 wyraża się wzorem
wyraża się wzorem 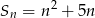 (
(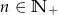 ). Drugi wyraz ciągu
). Drugi wyraz ciągu 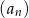 jest równy
jest równy
A) 2 B) 8 C) 12 D) 14
Suma ciągu arytmetycznego jest określona wzorem 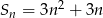 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 18 B) 3 C) 12 D) 15
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 6 jest równa
A) 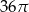 B)
B) 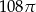 C)
C) 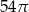 D)
D) 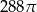
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 18 jest równa
A) 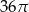 B)
B) 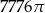 C)
C) 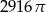 D)
D) 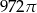
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 12 jest równa
A) 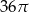 B)
B) 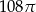 C)
C) 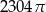 D)
D) 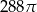
Cenę  pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę 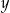 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 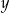 należy podnieść o
należy podnieść o
A) 100% B) 300% C) 75% D) 200%
Cenę  pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 20% i otrzymano cenę 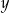 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 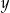 należy podnieść o
należy podnieść o
A) 40% B) 64% C) 75% D) 56,25%
Funkcja 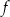 jest określona wzorem
jest określona wzorem 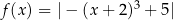 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Zbiorem wartości funkcji
. Zbiorem wartości funkcji 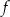 jest przedział
jest przedział
A) 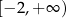 B)
B) 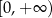 C)
C) 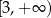 D)
D) 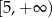
Ze zbioru 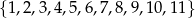 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 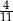 B)
B) 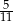 C)
C) 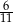 D)
D) 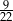
Ze zbioru liczb 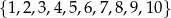 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru 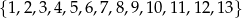 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 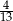 B)
B) 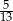 C)
C) 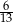 D)
D) 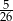
Ze zbioru 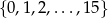 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 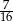 B)
B)  C)
C) 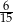 D)
D) 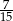
Promień podstawy stożka o objętości 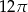 i wysokości 4 jest równy
i wysokości 4 jest równy
A) 1 B) 3 C) 6 D) 9
Nieskończony ciąg geometryczny 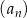 jest określony w następujący sposób:
jest określony w następujący sposób: 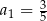 oraz
oraz 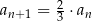 dla
dla 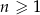 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 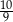 C)
C) 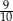 D)
D) 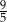
Nieskończony ciąg geometryczny 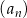 jest określony w następujący sposób:
jest określony w następujący sposób: 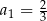 oraz
oraz 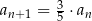 dla
dla 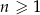 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 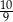 C)
C) 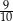 D)
D) 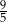
Równanie 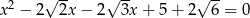
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Jeżeli ciąg 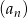 dany jest wzorem
dany jest wzorem 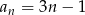 dla
dla 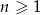 , to suma 10 początkowych wyrazów ciągu
, to suma 10 początkowych wyrazów ciągu 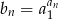 wyraża się wzorem
wyraża się wzorem
A) 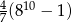 B)
B) 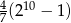 C)
C) 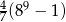 D)
D) 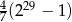
Okrąg, którego środkiem jest punkt 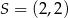 , jest styczny do prostej
, jest styczny do prostej 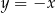 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 2 B) 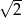 C)
C) 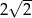 D) 4
D) 4
Dla której z podanych funkcji granica prawostronna 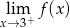 jest skończona?
jest skończona?
A) 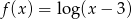 B)
B) 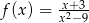 C)
C) 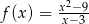 D)
D) 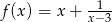
Dla której z podanych funkcji granica prawostronna 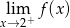 jest skończona?
jest skończona?
A) 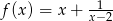 B)
B) 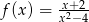 C)
C) 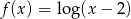 D)
D) 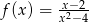
Funkcja 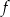 jest określona wzorem
jest określona wzorem 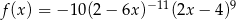 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 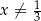 . Wartość funkcji
. Wartość funkcji 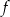 dla argumentu 2019 jest taka sama jak
dla argumentu 2019 jest taka sama jak 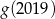 jeżeli
jeżeli
A) 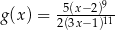 B)
B) 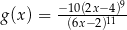
C) 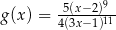 D)
D) 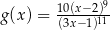
Iloczyn wszystkich rozwiązań równania 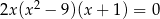 jest równy
jest równy
A) 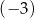 B) 3 C) 0 D) 9
B) 3 C) 0 D) 9
Ciąg 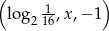 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 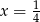 B)
B) 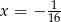 C)
C) 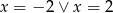 D)
D) 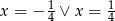
Ciąg 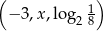 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 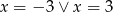 B)
B) 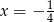 C)
C) 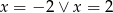 D)
D) 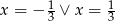
Ciąg 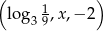 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 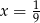 B)
B) 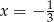 C)
C) 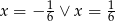 D)
D) 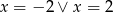
Czwarta potęga liczby 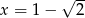 jest równa
jest równa
A) 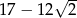 B)
B) 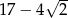 C)
C) 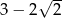 D)
D) 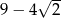
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Pan Henryk szykując się rano do pracy wybiera jeden spośród swoich 10 zegarków oraz dwa spośród 18 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 45 B) 46 C) 3240 D) 3060
Ciąg arytmetyczny 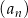 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 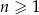 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 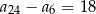 B)
B) 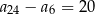 C)
C) 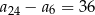 D)
D) 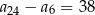
Ciąg arytmetyczny 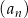 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 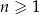 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa 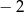 . Wtedy
. Wtedy
A) 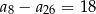 B)
B) 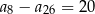 C)
C) 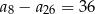 D)
D) 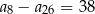
Wartość wyrażenia 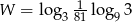 jest równa
jest równa
A) 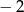 B)
B) 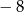 C)
C) 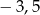 D)
D) 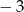
Wartość wyrażenia 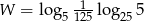 jest równa
jest równa
A) 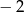 B)
B) 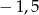 C)
C) 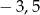 D)
D) 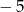
Wartość wyrażenia 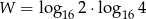 jest równa
jest równa
A) 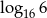 B)
B) 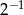 C)
C) 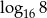 D)
D) 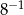
Wartość wyrażenia 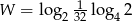 jest równa
jest równa
A) 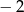 B)
B) 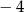 C)
C) 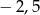 D)
D) 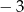
Obwód trójkąta równobocznego jest równy 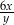 , gdzie
, gdzie 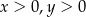 . Pole powierzchni tego trójkąta jest równe
. Pole powierzchni tego trójkąta jest równe
A) 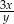 B)
B) 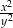 C)
C) 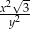 D)
D)