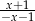Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,02% masy roztworu. Jaka była masa roztworu?
A) 2,5 kg B) 250 g C) 25 g D) 2,5 g
/Szkoła średnia/Zadania testowe
Badając pewien roztwór stwierdzono, że zawiera on 0,06 g chloru, co stanowi 0,04% masy roztworu. Jaka była masa roztworu?
A) 1,5 kg B) 15 g C) 150 g D) 1,5 g
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,01% masy roztworu. Jaka była masa roztworu?
A) 5 kg B) 50 g C) 500 g D) 5 g
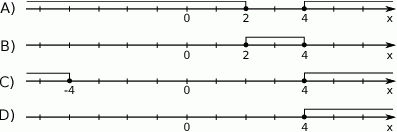
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 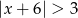 .
.
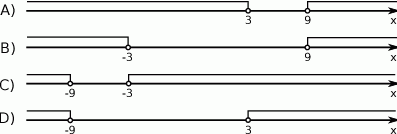
Zbiór rozwiązań nierówności 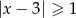 jest przedstawiony na rysunku
jest przedstawiony na rysunku
Zbiór rozwiązań nierówności 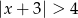 jest przedstawiony na rysunku
jest przedstawiony na rysunku
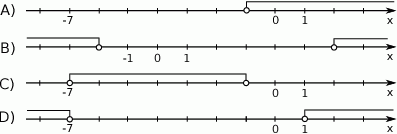
Zbiór wszystkich rozwiązań nierówności 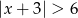 jest przedstawiony jako przedział na osi
jest przedstawiony jako przedział na osi
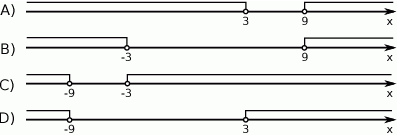
Dana jest nierówność
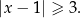
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność?

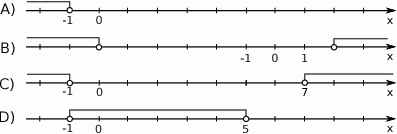
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 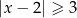 .
.

Zbiór rozwiązań nierówności 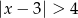 jest przedstawiony na rysunku
jest przedstawiony na rysunku
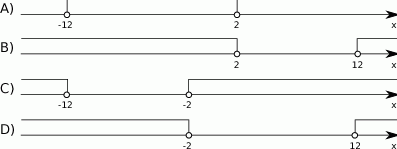
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 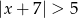 .
.
Ciąg 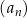 jest określony wzorem
jest określony wzorem 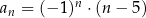 dla każdej liczby naturalnej
dla każdej liczby naturalnej 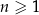 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwszy wyraz ciągu 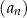 jest dwa razy większy od trzeciego wyrazu tego ciągu. jest dwa razy większy od trzeciego wyrazu tego ciągu. | P | F |
Wszystkie wyrazy ciągu 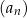 są dodatnie. są dodatnie. | P | F |
Jednym z miejsc zerowych funkcji kwadratowej 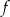 jest liczba
jest liczba 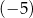 . Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji
. Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji 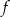 , jest równa 3. Drugim miejscem zerowym funkcji
, jest równa 3. Drugim miejscem zerowym funkcji 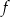 jest liczba
jest liczba
A) 11 B) 1 C) 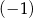 D)
D) 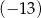
Jednym z miejsc zerowych funkcji kwadratowej 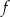 jest liczba
jest liczba 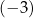 . Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji
. Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji 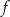 , jest równa 3. Drugim miejscem zerowym funkcji
, jest równa 3. Drugim miejscem zerowym funkcji 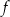 jest liczba
jest liczba
A) 6 B) 5 C) 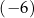 D) 9
D) 9
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
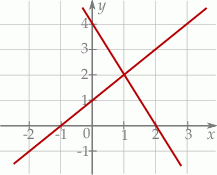
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 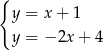 B)
B) 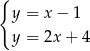 C)
C) 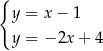 D)
D) 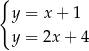
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
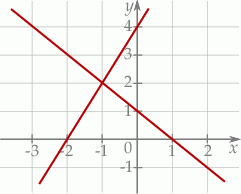
Wskaż ten układ
A) 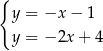 B)
B) 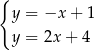 C)
C) 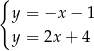 D)
D) 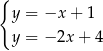
Na rysunku, w kartezjańskim układzie współrzędnych 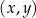 , przedstawiono interpretację geometryczną jednego z poniższych układów równań
, przedstawiono interpretację geometryczną jednego z poniższych układów równań
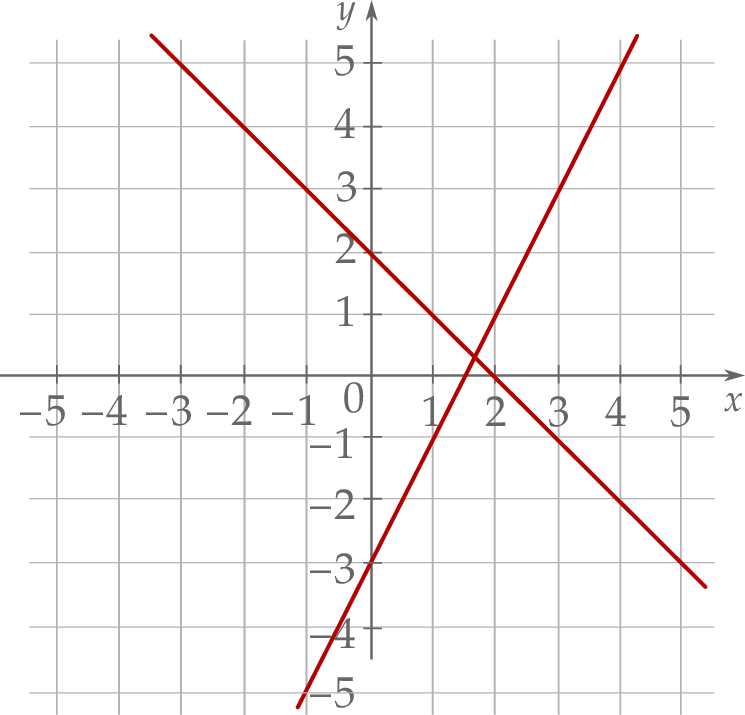
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 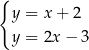 B)
B) 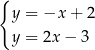 C)
C) 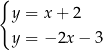 D)
D) 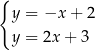
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 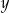 .
.
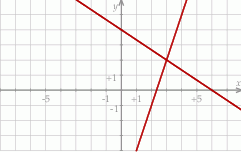
Wskaż ten układ
A) 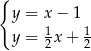 B)
B) 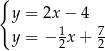 C)
C) 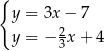 D)
D) 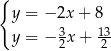
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
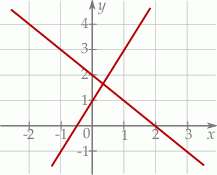
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 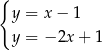 B)
B) 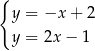 C)
C) 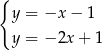 D)
D) 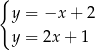
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
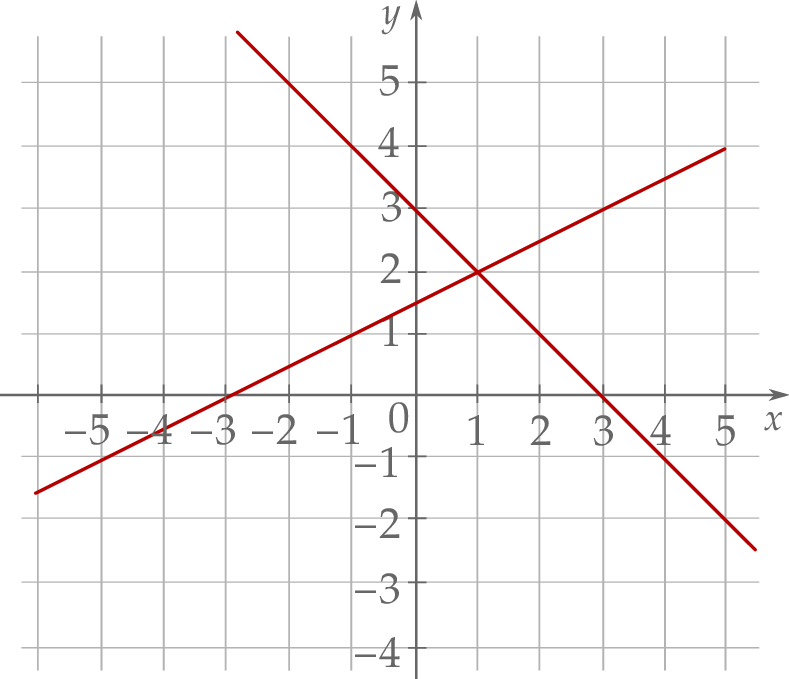
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 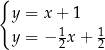 B)
B) 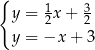 C)
C) 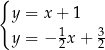 D)
D) 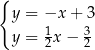
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
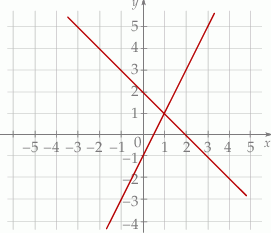
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 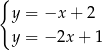 B)
B) 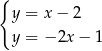 C)
C) 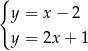 D)
D) 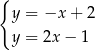
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 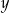 .
.
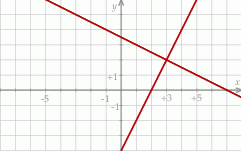
Wskaż ten układ
A) 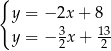 B)
B) 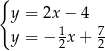 C)
C) 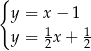 D)
D) 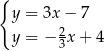
Na rysunku, w kartezjańskim układzie współrzędnych 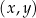 , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
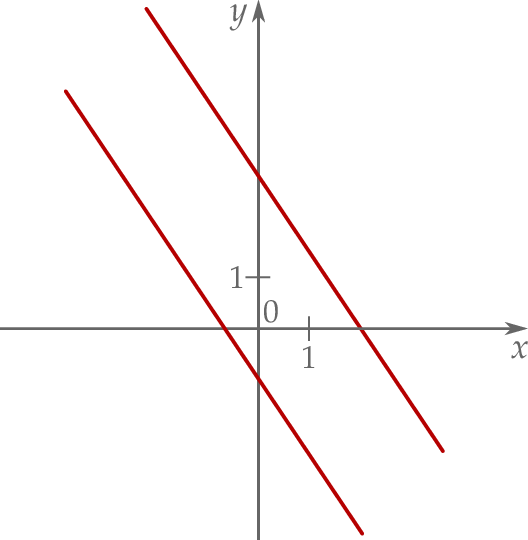
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 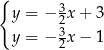 B)
B) 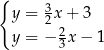
C) 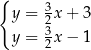 D)
D) 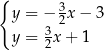
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest równy 70?
A) 60 B) 36 C) 12 D) 125
Pole powierzchni pokoju jest równe 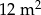 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
A) 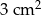 B)
B) 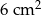 C)
C) 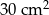 D)
D) 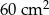
Pole działki budowlanej jest równe 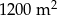 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 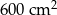 B)
B) 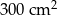 C)
C) 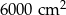 D)
D) 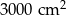
Pole powierzchni pokoju jest równe 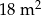 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:300 wynosi:
A) 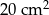 B)
B) 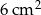 C)
C) 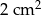 D)
D) 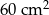
Pole działki budowlanej jest równe 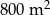 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 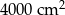 B)
B) 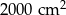 C)
C) 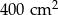 D)
D) 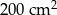
Pole powierzchni pokoju jest równe 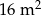 . Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tego pokoju na planie wykonanym w skali 1:200 wynosi:
A) 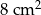 B)
B) 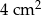 C)
C) 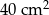 D)
D) 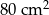
Wskaż wartość parametru 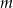 , dla którego prosta
, dla którego prosta 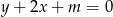 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 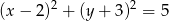
A) 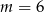 B)
B) 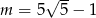 C)
C) 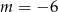 D)
D) 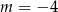
Wskaż wartość parametru 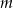 , dla którego prosta
, dla którego prosta 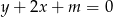 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 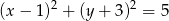
A) 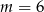 B)
B) 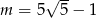 C)
C) 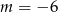 D)
D) 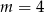
Przyprostokątna 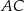 trójkąta prostokątnego
trójkąta prostokątnego 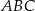 ma długość 6, a wysokość
ma długość 6, a wysokość 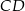 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 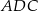 i
i 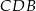 , że pole trójkąta
, że pole trójkąta 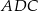 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 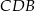 (zobacz rysunek).
(zobacz rysunek).
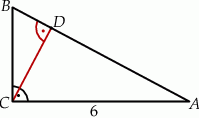
Przyprostokątna 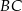 trójkąta prostokątnego
trójkąta prostokątnego 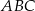 jest równa
jest równa
A) 1,5 B) 2 C) 2,5 D) 3
Przyprostokątna 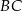 trójkąta prostokątnego
trójkąta prostokątnego 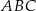 ma długość 6, a wysokość
ma długość 6, a wysokość 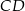 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 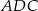 i
i 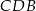 , że pole trójkąta
, że pole trójkąta 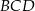 jest 4 razy mniejsze od pola trójkąta
jest 4 razy mniejsze od pola trójkąta 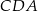 (zobacz rysunek).
(zobacz rysunek).
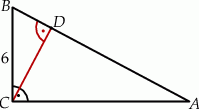
Przyprostokątna 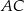 trójkąta prostokątnego
trójkąta prostokątnego 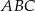 jest równa
jest równa
A) 12 B) 8 C) 9 D) 24
Trzywyrazowy ciąg 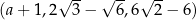 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 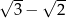 B)
B) 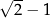 C)
C) 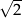 D)
D) 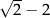
Liczba 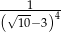 jest równa
jest równa
A) 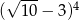 B)
B) 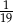 C)
C) 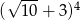 D)
D) 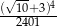
Liczba 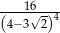 jest równa
jest równa
A) 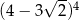 B)
B) 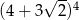 C)
C) 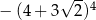 D)
D) 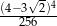
Liczba rozwiązań równania 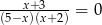 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Równanie 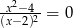
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Liczba rozwiązań równania 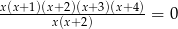 jest równa
jest równa
A) 6 B) 5 C) 4 D) 3
Liczba miejsc zerowych funkcji 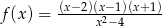 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 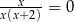 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Wskaż liczbę rozwiązań równania 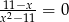 .
.
A) 0 B) 1 C) 2 D) 3
Równanie 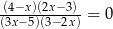 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Równanie 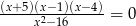
A) nie ma pierwiastków
B) ma jeden pierwiastek
C) ma dwa pierwiastki
D) ma trzy pierwiastki
Równanie 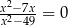 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Liczba rozwiązań równania 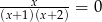 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 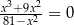 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 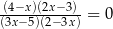 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Równanie 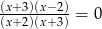 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 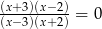 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 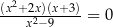 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) cztery rozwiązania. B) trzy rozwiązania.
C) dwa rozwiązania. D) jedno rozwiązanie.
Równanie 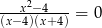
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 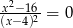
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 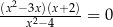 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Dany jest wykres funkcji 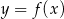 . Dziedziną
. Dziedziną 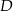 i zbiorem wartości
i zbiorem wartości 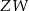 tej funkcji jest
tej funkcji jest
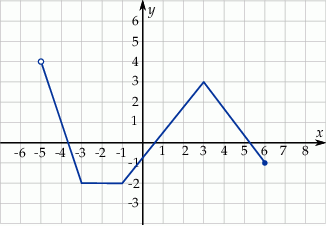
A) 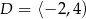 ,
, 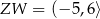 B)
B) 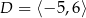 ,
, 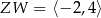
C) 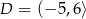 ,
, 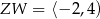 D)
D) 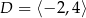 ,
, 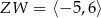
Dany jest wykres funkcji 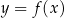 . Dziedziną
. Dziedziną 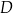 i zbiorem wartości
i zbiorem wartości 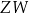 tej funkcji jest
tej funkcji jest
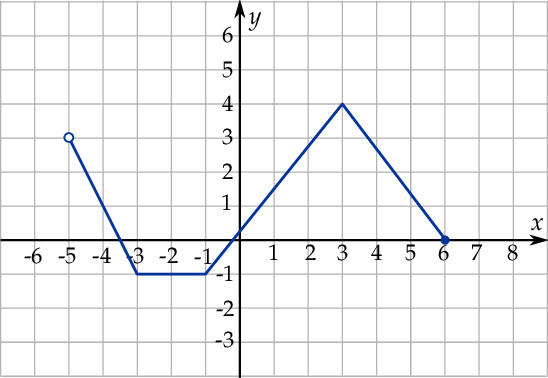
A) 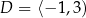 ,
, 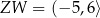 B)
B) 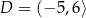 ,
, 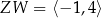
C) 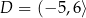 ,
, 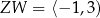 D)
D) 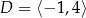 ,
, 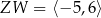
Przesuwając wykres funkcji 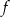 wzdłuż osi
wzdłuż osi 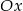 o 6 jednostek w prawo, otrzymano wykres funkcji
o 6 jednostek w prawo, otrzymano wykres funkcji 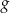 . Zatem
. Zatem
A) 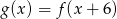 B)
B) 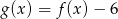 C)
C) 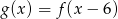 D)
D) 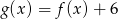
Przesuwając wykres funkcji 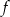 wzdłuż osi
wzdłuż osi 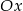 o 6 jednostek w lewo, otrzymano wykres funkcji
o 6 jednostek w lewo, otrzymano wykres funkcji 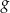 . Zatem
. Zatem
A) 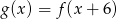 B)
B) 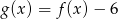 C)
C) 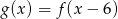 D)
D) 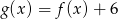
Okręgi 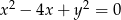 i
i 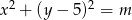 , gdzie
, gdzie 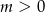 są styczne zewnętrznie. Zatem
są styczne zewnętrznie. Zatem
A) 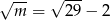 B)
B) 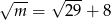 C)
C) 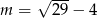 D)
D) 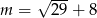
Granica 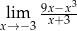 jest równa
jest równa
A) 0 B) 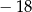 C)
C) 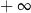 D)
D) 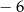
Granica 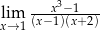 jest równa
jest równa
A) 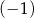 B) 0 C)
B) 0 C) 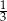 D) 1
D) 1
Jacek planując wycieczkę zagraniczną postanowił ocenić kilka ofert przyznając punkty w trzech kategoriach
| Nr oferty | Cena | Atrakcyjność | Dostępność |
| I | 1 | 3 | 4 |
| II | 2 | 2 | 2 |
| III | 3 | 1 | 2 |
Aby porównać ze sobą oferty postanowił policzyć średnią ważoną przyznanych punktów stosując następujące wagi:
| Kategoria | Cena | Atrakcyjność | Dostępność |
| Waga | 50 | 35 | 15 |
Wycieczki, dla których policzona średnia jest najwyższa to
A) I i II B) II i III C) I i III D) III
Aby na podstawie wykresu funkcji 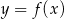 narysować wykres funkcji
narysować wykres funkcji 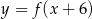 , należy wykres funkcji
, należy wykres funkcji 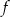 przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Aby na podstawie wykresu funkcji 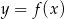 narysować wykres funkcji
narysować wykres funkcji 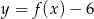 , należy wykres funkcji
, należy wykres funkcji  przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Aby na podstawie wykresu funkcji 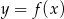 narysować wykres funkcji
narysować wykres funkcji 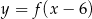 , należy wykres funkcji
, należy wykres funkcji 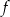 przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Punkty 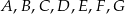 są wierzchołkami siedmiokąta foremnego.
są wierzchołkami siedmiokąta foremnego.
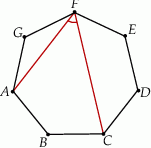
Miara zaznaczonego na rysunku kąta 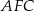 jest równa
jest równa
A) 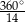 B)
B) 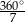 C)
C) 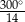 D)
D) 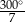
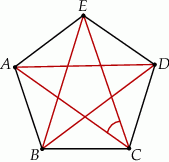
Punkty 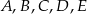 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta 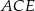 jest równa
jest równa
A) 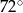 B)
B) 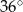 C)
C) 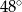 D)
D) 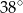
Wyrażenie wymierne 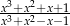 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 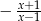 B)
B) 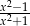 C)
C) 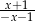 D)
D) 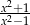
Wyrażenie wymierne 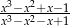 po uproszczeniu ma postać:
po uproszczeniu ma postać:
A) 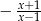 B)
B) 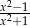 C)
C) 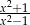 D)
D)