W ciągu arytmetycznym 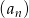 , określonym dla
, określonym dla 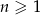 , dane są dwa wyrazy:
, dane są dwa wyrazy: 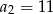 i
i 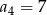 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
/Szkoła średnia/Zadania testowe
W ciągu arytmetycznym 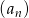 , określonym dla
, określonym dla 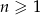 , dane są dwa wyrazy:
, dane są dwa wyrazy: 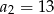 i
i 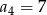 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 92 B) 39 C) 46 D) 50
Niech 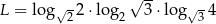 . Wtedy
. Wtedy
A) 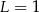 B)
B) 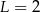 C)
C) 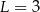 D)
D) 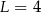
Niech 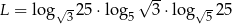 . Wtedy
. Wtedy
A) 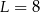 B)
B) 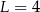 C)
C) 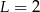 D)
D) 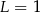
Suma kwadratów liczb 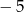 i
i 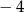 jest równa:
jest równa:
A) 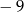 B) 81 C) 41 D)
B) 81 C) 41 D) 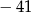
20% pola ograniczonego okręgiem o równaniu 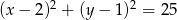 wynosi
wynosi
A) 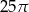 B)
B) 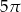 C)
C) 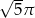 D)
D) 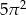
Prawdopodobieństwo zdarzenia 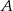 jest równe
jest równe 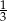 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 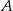 i
i 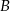 jest równe
jest równe 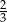 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 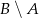 jest równe
jest równe
A) 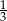 B)
B)  C)
C) 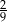 D)
D) 
Jeżeli 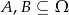 oraz
oraz 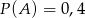 i
i 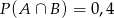 to prawdopodobieństwo
to prawdopodobieństwo 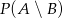 jest równe
jest równe
A) 0,6 B) 0,4 C) 1 D) 0
Prawdopodobieństwo zdarzenia 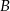 jest równe
jest równe 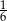 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 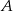 i
i 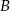 jest równe
jest równe 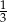 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 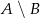 jest równe
jest równe
A) 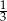 B)
B)  C)
C)  D)
D) 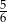
Liczba 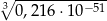 jest równa
jest równa
A) 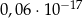 B)
B) 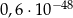 C)
C) 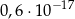 D)
D) 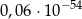
Liczba 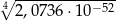 jest równa
jest równa
A) 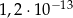 B)
B) 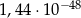 C)
C) 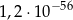 D)
D) 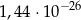
Okrąg wpisany w trójkąt równoboczny ma promień równy 6. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 36 D) 24
Okrąg wpisany w trójkąt równoboczny ma promień równy 8. Wysokość tego trójkąta jest równa
A) 12 B) 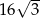 C)
C) 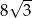 D) 24
D) 24
Dany jest ciąg 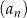 określony wzorem
określony wzorem 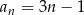 dla każdej liczby naturalnej
dla każdej liczby naturalnej 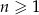 . Ciąg
. Ciąg 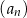 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 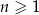
1) 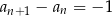 , , | 2) 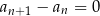 , , | 3) 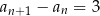 , , |
Dany jest ciąg 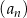 określony wzorem
określony wzorem 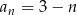 dla każdej liczby naturalnej
dla każdej liczby naturalnej 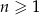 . Ciąg
. Ciąg 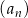 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 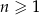
1) 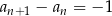 , , | 2) 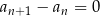 , , | 3) 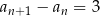 , , |
Wyraz wolny wielomianu 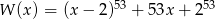 jest równy
jest równy
A) 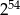 B) 0 C)
B) 0 C) 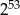 D) 53
D) 53
Wyraz wolny wielomianu 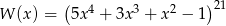 (po uporządkowaniu) jest równy
(po uporządkowaniu) jest równy
A) 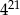 B)
B) 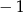 C) 1 D)
C) 1 D) 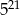
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 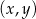 , dany jest okrąg
, dany jest okrąg 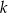 o środku
o środku 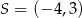 . Jednym z punktów leżących na tym okręgu jest
. Jednym z punktów leżących na tym okręgu jest 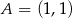 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Punkt 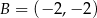 należy do okręgu należy do okręgu 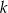 . . | P | F |
Promień okręgu 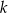 jest równy 29. jest równy 29. | P | F |
Średnice 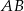 i
i 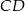 okręgu o środku
okręgu o środku 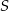 przecinają się pod kątem
przecinają się pod kątem 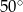 (tak jak na rysunku).
(tak jak na rysunku).
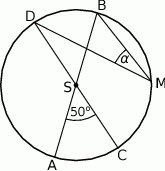
Miara kąta  jest równa
jest równa
A) 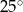 B)
B) 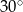 C)
C) 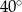 D)
D) 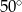
Średnice 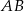 i
i 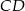 okręgu o środku
okręgu o środku 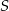 przecinają się pod kątem
przecinają się pod kątem 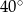 (tak jak na rysunku).
(tak jak na rysunku).
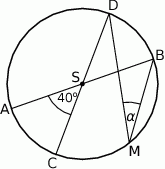
Miara kąta  jest równa
jest równa
A) 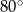 B)
B) 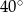 C)
C) 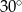 D)
D) 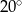
Średnia arytmetyczna liczb: 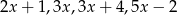 i
i 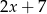 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 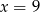 B)
B) 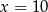 C)
C) 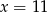 D)
D) 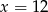
Średnia arytmetyczna liczb: 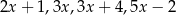 i
i 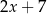 zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 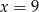 B)
B) 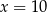 C)
C) 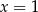 D)
D) 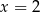
Średnia arytmetyczna liczb: 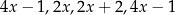 i
i 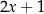 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 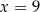 B)
B) 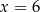 C)
C) 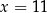 D)
D) 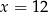
W każdym z czterech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 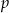 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
A) 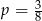 B)
B) 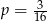 C)
C) 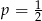 D)
D) 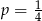
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie trzy razy w czterech losowaniach wyciągniemy kulę koloru białego, jest równe
A) 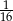 B)
B)  C)
C) 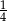 D)
D) 
W każdym z pięciu pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 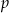 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
A) 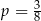 B)
B) 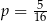 C)
C) 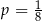 D)
D) 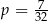
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy w czterech losowaniach wyciągniemy kulę koloru czarnego, jest równe
A) 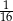 B)
B)  C)
C) 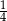 D)
D) 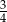
Dla której z podanych wartości  , wykres funkcji
, wykres funkcji 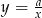 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 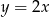 ?
?
A) 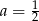 B)
B) 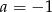 C)
C) 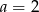 D)
D) 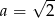
Liczby 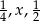 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 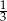 B)
B)  C)
C) 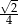 D)
D) 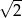
Ciąg 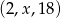 jest ciągiem geometrycznym tylko wtedy, gdy
jest ciągiem geometrycznym tylko wtedy, gdy
A) 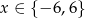 B)
B) 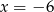 C)
C) 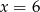 D)
D) 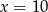
Trzywyrazowy ciąg 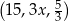 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 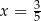 B)
B) 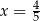 C)
C) 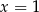 D)
D) 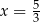
Trójwyrazowy ciąg 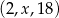 jest rosnącym ciągiem geometrycznym. Wtedy
jest rosnącym ciągiem geometrycznym. Wtedy
A) 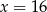 B)
B) 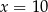 C)
C) 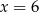 D)
D) 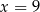
Liczby 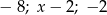 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  może być równa
może być równa
A) 4 B) 6 C) 7 D) 8
Trzywyrazowy ciąg 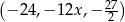 jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
A) 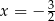 B)
B) 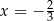 C)
C) 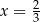 D)
D) 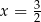
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 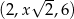 . Wówczas
. Wówczas
A) 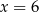 B)
B) 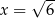 C)
C) 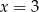 D)
D) 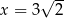
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 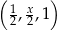 . Wówczas
. Wówczas
A) 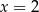 B)
B) 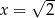 C)
C) 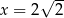 D)
D) 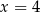
Liczby 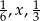 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 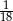 B)
B) 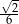 C)
C) 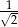 D)
D) 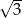
Jeżeli liczby 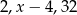 tworzą rosnący ciąg geometryczny, to
tworzą rosnący ciąg geometryczny, to
A) 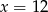 B)
B) 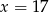 C)
C) 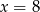 D)
D) 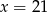
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 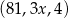 . Stąd wynika, że
. Stąd wynika, że
A) 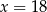 B)
B) 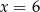 C)
C) 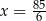 D)
D) 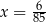
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 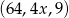 . Stąd wynika, że
. Stąd wynika, że
A) 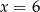 B)
B) 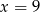 C)
C) 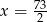 D)
D) 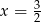
Liczby 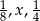 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 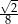 B)
B) 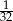 C)
C) 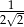 D)
D) 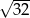
Liczby 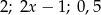 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
A) 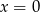 B)
B) 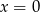 lub
lub 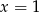 C)
C) 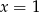 D)
D) 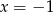
Ciąg 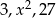 jest ciągiem geometrycznym, gdy
jest ciągiem geometrycznym, gdy
A) tylko 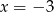 B) tylko
B) tylko 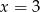 C)
C) 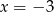 lub
lub 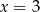 D)
D) 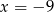 lub
lub 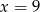
Funkcja 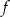 określona jest wzorem
określona jest wzorem 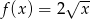 dla
dla 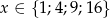 . Do zbioru wartości tej funkcji nie należy liczba
. Do zbioru wartości tej funkcji nie należy liczba
A) 2 B) 5 C) 6 D) 4
Odcinek o końcach 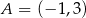 i
i 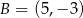 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu
A) 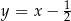 B)
B) 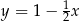 C)
C) 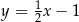 D)
D) 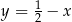
W pewnym mieście na czas festynu postanowiono rozstawić stragany. Ustalono, że będzie można ustawić po 3 stragany po każdej stronie drogi. Na ile sposobów można ustawić te stragany?
A) 6 B) 24 C) 36 D) 720
W trakcie zawodów sportowych ośmioro uczniów miało ustawić się w dwóch rzędach po 4 osoby. Na ile sposobów mogą ustawić się ci uczniowie?
A) 4 B) 576 C) 40320 D) 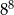
W rosnącym ciągu geometrycznym stosunek wyrazu czwartego do drugiego jest równy 8. Iloraz tego ciągu jest równy
A) 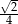 B) 4 C)
B) 4 C) 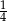 D)
D) 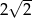
Dany jest ciąg geometryczny 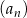 , określony dla
, określony dla 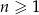 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 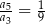 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 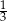 B)
B) 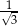 C) 3 D)
C) 3 D) 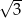
Dany jest ciąg geometryczny 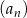 , określony dla
, określony dla 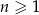 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 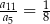 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 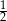 B)
B) 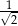 C)
C) 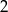 D)
D) 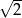
Dany jest ciąg 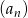 określony wzorem
określony wzorem 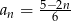 dla
dla 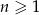 . Ciąg ten jest
. Ciąg ten jest
A) arytmetyczny i jego różnica jest równa 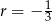 .
.
B) arytmetyczny i jego różnica jest równa 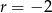 .
.
C) geometryczny i jego iloraz jest równy 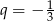 .
.
D) geometryczny i jego iloraz jest równy 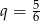 .
.
Dany jest ciąg 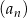 określony wzorem
określony wzorem 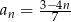 dla
dla 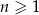 . Ciąg ten jest
. Ciąg ten jest
A) geometryczny i jego iloraz jest równy 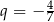 .
.
B) geometryczny i jego iloraz jest równy 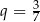 .
.
C) arytmetyczny i jego różnica jest równa 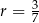 .
.
D) arytmetyczny i jego różnica jest równa 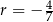 .
.

