Z odcinków o długościach: 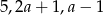 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 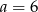 B)
B) 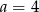 C)
C) 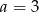 D)
D) 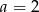
/Szkoła średnia/Zadania testowe
Z odcinków o długościach: 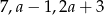 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 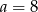 B)
B) 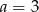 C)
C) 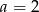 D)
D) 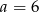
Dane są liczby 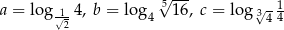 . Liczby te spełniają warunek
. Liczby te spełniają warunek
A) 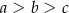 B)
B) 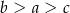 C)
C) 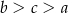 D)
D) 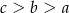
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 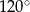 B)
B) 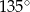 C)
C) 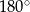 D)
D) 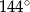
Na diagramie przestawiono wzrost pięciorga uczniów.
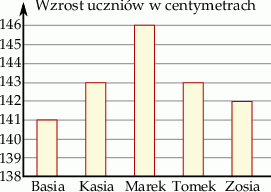
Odchylenie standardowe zestawu danych jest równe
A) 2 cm B) 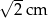 C)
C) 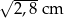 D) 2,8 cm
D) 2,8 cm
Proste o równaniach: 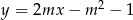 oraz
oraz 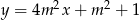 są prostopadłe dla
są prostopadłe dla
A) 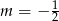 B)
B) 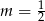 C)
C) 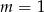 D)
D) 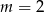
Proste opisane równaniami 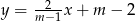 oraz
oraz 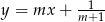 są prostopadłe, gdy
są prostopadłe, gdy
A) 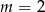 B)
B) 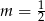 C)
C) 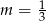 D)
D) 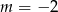
Proste opisane równaniami 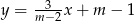 oraz
oraz 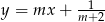 są prostopadłe, gdy
są prostopadłe, gdy
A) 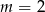 B)
B) 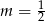 C)
C) 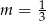 D)
D) 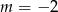
Proste o równaniach 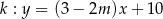 i
i 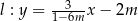 są prostopadłe dla
są prostopadłe dla
A) 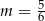 B)
B) 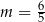 C)
C) 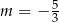 D)
D) 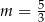
Proste o równaniach: 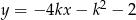 oraz
oraz 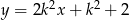 są prostopadłe dla
są prostopadłe dla
A) 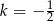 B)
B) 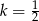 C)
C) 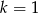 D)
D) 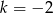
Prosta o równaniu 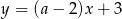 jest prostopadła do prostej
jest prostopadła do prostej 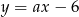 . Zatem
. Zatem
A) 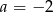 B)
B) 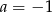 C)
C) 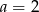 D)
D) 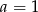
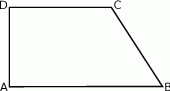
Długość ramienia 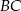 trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt 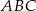 ma miarę
ma miarę
A) 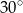 B)
B) 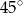 C)
C) 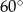 D)
D) 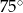
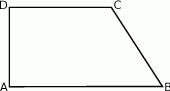
Długość ramienia 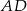 trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt 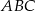 ma miarę
ma miarę
A) 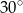 B)
B) 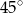 C)
C) 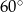 D)
D) 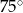
Liczba ścian graniastosłupa, który ma 14 wierzchołków, jest równa
A) 7 B) 5 C) 9 D) 11
Liczba ścian graniastosłupa, który ma 16 wierzchołków, jest równa
A) 12 B) 10 C) 9 D) 8
Liczba ścian graniastosłupa, który ma 20 wierzchołków, jest równa
A) 12 B) 10 C) 5 D) 8
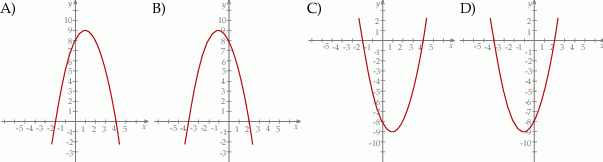
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 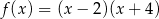 .
.
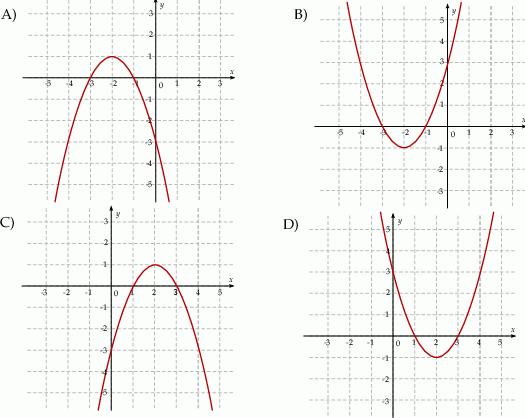
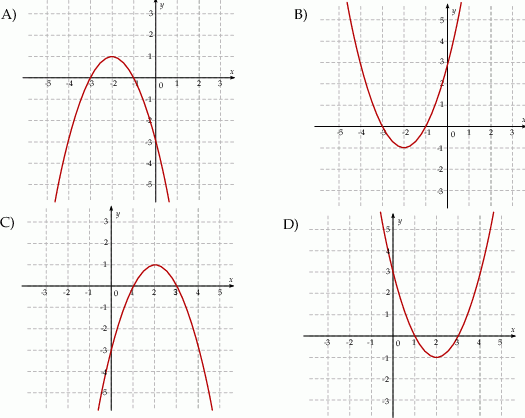
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 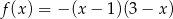 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 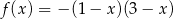 . Wskaż ten rysunek.
. Wskaż ten rysunek.
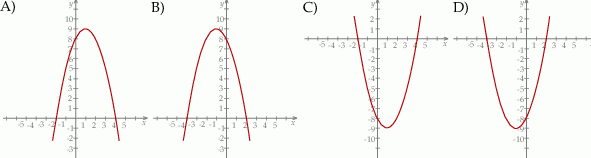
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 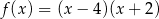 .
.
Pole równoległoboku o bokach długości 4 i 12 oraz kącie ostrym 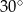 jest równe
jest równe
A) 24 B) 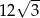 C) 12 D)
C) 12 D) 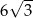
Pole równoległoboku o bokach długości 6 i 10 oraz kącie ostrym 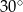 jest równe
jest równe
A) 60 B) 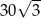 C) 30 D)
C) 30 D) 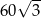
Pole równoległoboku o kącie ostrym równym 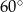 i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
i długości boków wychodzących z wierzchołka tego kąta równych 6 i 8 jest równe
A) 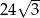 B)
B) 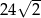 C) 24 D)
C) 24 D) 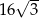
Liczba 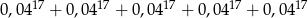 jest równa
jest równa
A) 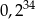 B)
B)  C)
C) 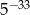 D)
D) 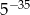
Liczba 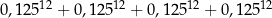 jest równa
jest równa
A) 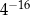 B)
B) 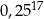 C)
C) 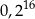 D)
D) 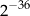
Suma odległości punktu 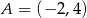 od prostych o równaniach
od prostych o równaniach 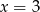 i
i 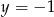 jest równa
jest równa
A) 10 B) 9 C) 8 D) 7
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 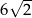 , a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
, a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
A) 6 B) 8 C) 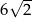 D)
D) 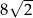
Drabinę o długości 4 metrów oparto o pionowy mur, a jej podstawę umieszczono w odległości 1,30 m od tego muru (zobacz rysunek).
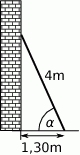
Kąt  , pod jakim ustawiono drabinę, spełnia warunek
, pod jakim ustawiono drabinę, spełnia warunek
A) 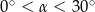 B)
B) 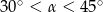 C)
C) 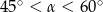 D)
D) 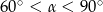
Różnica 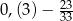 jest równa
jest równa
A) 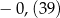 B)
B) 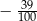 C)
C) 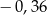 D)
D) 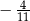
Różnica 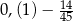 jest równa
jest równa
A) 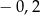 B)
B) 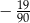 C)
C) 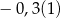 D)
D) 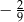
Z odcinków 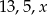 budujemy trójkąt. Będzie on prostokątny, gdy:
budujemy trójkąt. Będzie on prostokątny, gdy:
A) 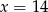 B)
B) 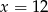 C)
C) 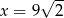 D)
D) 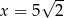
Na planie miasta, narysowanym w skali 1:20 000, park jest prostokątem o bokach 2 cm i 5 cm. Stąd wynika, że ten park ma powierzchnię
A) 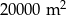 B)
B) 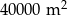 C)
C) 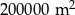 D)
D) 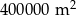
Na planie miasta, narysowanym w skali 1:25 000, park jest prostokątem o bokach 2 cm i 4 cm. Stąd wynika, że ten park ma powierzchnię
A) 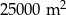 B)
B) 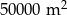 C)
C) 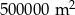 D)
D) 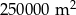
Punkty 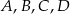 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 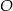 . Kąt środkowy
. Kąt środkowy 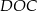 ma miarę
ma miarę 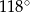 (zobacz rysunek).
(zobacz rysunek).
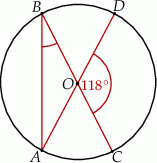
Miara kąta 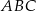 jest równa
jest równa
A) 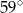 B)
B) 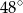 C)
C) 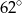 D)
D) 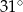
Punkty 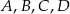 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 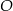 . Kąt środkowy
. Kąt środkowy 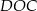 ma miarę
ma miarę 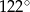 (zobacz rysunek).
(zobacz rysunek).
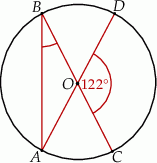
Miara kąta 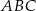 jest równa
jest równa
A) 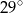 B)
B) 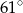 C)
C) 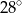 D)
D) 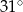
W pewnym trójkącie równoramiennym największy kąt ma miarę 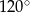 , a najdłuższy bok ma długość 12 (zobacz rysunek).
, a najdłuższy bok ma długość 12 (zobacz rysunek).
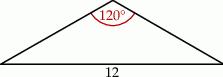
Najkrótsza wysokość tego trójkąta ma długość równą
A) 6 B) 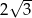 C)
C) 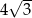 D)
D) 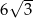
W pewnym trójkącie równoramiennym największy kąt ma miarę 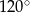 , a ramię ma długość 6 (zobacz rysunek).
, a ramię ma długość 6 (zobacz rysunek).

Najkrótsza wysokość tego trójkąta ma długość równą
A) 4 B) 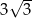 C)
C) 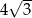 D) 3
D) 3
Liczby  i
i 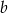 są liczbami o przeciwnych znakach. Liczba punktów wspólnych wykresu funkcji
są liczbami o przeciwnych znakach. Liczba punktów wspólnych wykresu funkcji 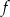 określonej wzorem
określonej wzorem 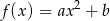 z prostą
z prostą 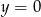 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczby  i
i 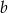 są liczbami niezerowymi o jednakowych znakach. Liczba punktów wspólnych wykresu funkcji
są liczbami niezerowymi o jednakowych znakach. Liczba punktów wspólnych wykresu funkcji 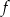 określonej wzorem
określonej wzorem 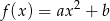 z prostą
z prostą 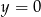 jest równa
jest równa
A) 1 B) 2 C) 3 D) 0
Liczby  i
i 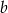 są liczbami o przeciwnych znakach. Liczba punktów wspólnych wykresu funkcji
są liczbami o przeciwnych znakach. Liczba punktów wspólnych wykresu funkcji 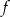 określonej wzorem
określonej wzorem 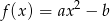 z prostą
z prostą 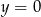 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Dany jest prostokąt o wymiarach 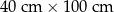 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Dany jest prostokąt o wymiarach 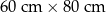 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 2% B) zwiększy się o 1%
C) zmniejszy się o 1% D) zmniejszy się o 2%

