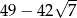Funkcja 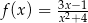 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Pochodna tej funkcji jest określona wzorem
. Pochodna tej funkcji jest określona wzorem
A) 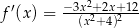 B)
B) 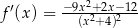
C) 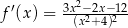 D)
D) 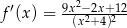
/Szkoła średnia/Zadania testowe
Funkcja 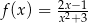 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Pochodna tej funkcji jest określona wzorem
. Pochodna tej funkcji jest określona wzorem
A) 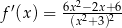 B)
B) 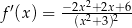
C) 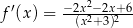 D)
D) 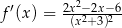
Pochodna 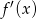 funkcji
funkcji 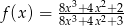 jest określona wzorem
jest określona wzorem
A) 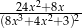 B)
B) 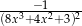 C)
C) 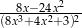 D)
D) 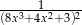
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość
A) 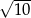 B)
B) 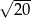 C)
C) 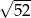 D) 10
D) 10
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 6 i wysokość jest równa 9, ma długość
A) 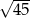 B) 15 C)
B) 15 C) 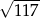 D) 10
D) 10
Jednym z rozwiązań równania 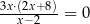 jest liczba
jest liczba
A) 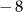 B)
B) 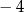 C) 2 D) 3
C) 2 D) 3
Ile wynosi tangens kąta  zaznaczonego na rysunku poniżej?
zaznaczonego na rysunku poniżej?
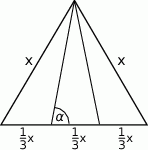
A) 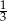 B)
B) 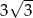 C)
C) 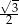 D)
D) 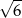
W kartezjańskim układzie współrzędnych 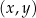 punkt
punkt 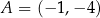 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 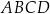 . Punkt
. Punkt 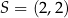 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 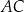 równoległoboku
równoległoboku 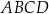 jest równa
jest równa
A) 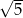 B)
B) 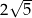 C)
C) 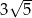 D)
D) 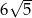
W kartezjańskim układzie współrzędnych 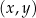 punkt
punkt 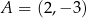 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 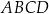 . Punkt
. Punkt 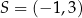 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 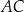 równoległoboku
równoległoboku 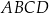 jest równa
jest równa
A) 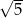 B)
B) 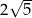 C)
C) 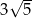 D)
D) 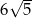
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 60 chłopców więcej niż dziewcząt. Chłopcy stanowili 65% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu?
A) 200 B) 130 C) 70 D) 39
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 20 chłopców mniej niż dziewcząt. Chłopcy stanowili 45% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu?
A) 140 B) 110 C) 120 D) 90
Trójkąt prostokątny równoramienny 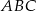 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 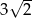 , jest podobny do trójkąta
, jest podobny do trójkąta 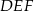 w skali
w skali 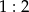 . Obwód trójkąta
. Obwód trójkąta 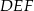 jest równy
jest równy
A) 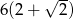 B)
B) 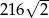 C)
C) 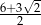 D)
D) 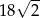
Trójkąt prostokątny równoramienny 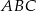 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 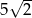 , jest podobny do trójkąta
, jest podobny do trójkąta 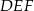 w skali
w skali 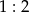 . Obwód trójkąta
. Obwód trójkąta 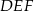 jest równy
jest równy
A) 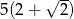 B)
B) 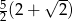 C)
C) 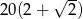 D)
D) 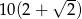
Trójkąt prostokątny równoramienny 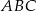 , w którym przeciwprostokątna jest równa
, w którym przeciwprostokątna jest równa 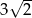 , jest podobny do trójkąta
, jest podobny do trójkąta 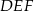 w skali
w skali 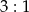 . Obwód trójkąta
. Obwód trójkąta 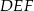 jest równy
jest równy
A) 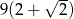 B)
B) 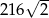 C)
C) 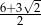 D)
D) 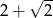
Kąt  jest ostry i
jest ostry i 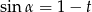 . Wtedy
. Wtedy
A) 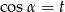 B)
B) 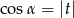 C)
C) 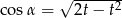 D)
D) 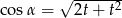
Kąt  jest ostry i
jest ostry i 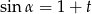 . Wtedy
. Wtedy
A) 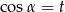 B)
B) 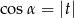 C)
C) 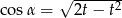 D)
D) 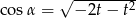
Ze zbioru liczb całkowitych, które są zawarte w przedziale 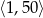 losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
A) 0,0048 B) 0,0028 C) 0,0024 D) 0,0052
Dana jest funkcja kwadratowa 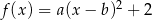 , gdzie
, gdzie 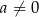 i
i 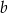 są liczbami rzeczywistymi. Funkcja
są liczbami rzeczywistymi. Funkcja 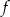 nie przyjmuje wartości większych od 2. Funkcja
nie przyjmuje wartości większych od 2. Funkcja 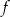
| A) ma miejsca zerowe, | B) nie ma miejsc zerowych, |
| ponieważ | |
| 1) | 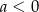 i i 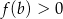 . . |
| 2) | 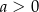 i i 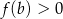 . . |
| 3) | 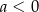 i i 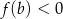 . . |
Objętość ostrosłupa prawidłowego czworokątnego jest równa 64. Wysokość tego ostrosłupa jest równa 12. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 2 B) 4 C) 6 D) 8
Dany jest ciąg arytmetyczny 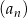 określony wzorem
określony wzorem 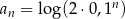 dla każdej liczby naturalnej
dla każdej liczby naturalnej 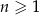 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 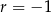 B)
B) 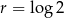 C)
C) 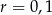 D)
D) 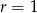
Równanie 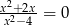
A) ma trzy rozwiązania: 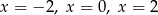
B) ma dwa rozwiązania: 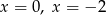
C) ma dwa rozwiązania: 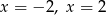
D) ma jedno rozwiązanie: 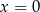
Równanie 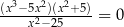 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Równanie 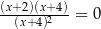 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 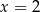 B) jedno rozwiązanie:
B) jedno rozwiązanie: 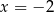
C) dwa rozwiązania: 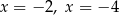 D) dwa rozwiązania:
D) dwa rozwiązania: 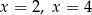
Równanie 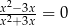
A) ma trzy rozwiązania: 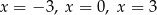
B) ma jedno rozwiązanie: 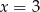
C) ma dwa rozwiązania: 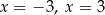
D) ma dwa rozwiązania: 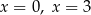
Równanie
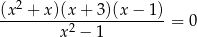
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 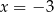
B) dwa rozwiązania: 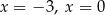
C) trzy rozwiązania: 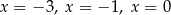
D) cztery rozwiązania: 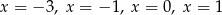
Równanie 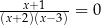 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie: 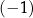 .
.
C) ma dokładnie dwa rozwiązania: 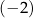 oraz 3.
oraz 3.
D) ma dokładnie trzy rozwiązania: 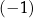 ,
, 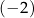 oraz 3.
oraz 3.
Równanie 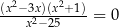 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Funkcja 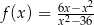
A) ma jedno miejsce zerowe 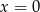
B) ma dwa miejsca zerowe: 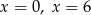
C) ma dwa miejsce zerowe: 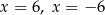
D) ma trzy miejsca zerowe: 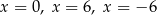
Równanie 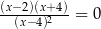 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 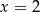 B) jedno rozwiązanie:
B) jedno rozwiązanie: 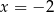
C) dwa rozwiązania: 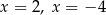 D) dwa rozwiązania:
D) dwa rozwiązania: 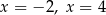
Równanie
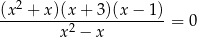
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 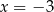
B) dwa rozwiązania: 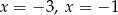
C) trzy rozwiązania: 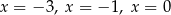
D) cztery rozwiązania: 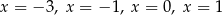
Najmniejszą liczbą całkowitą 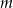 , dla której nierówność:
, dla której nierówność: 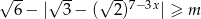 jest sprzeczna jest
jest sprzeczna jest
A) 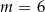 B)
B) 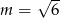 C)
C) 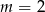 D)
D) 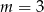
Największą wartością funkcji kwadratowej 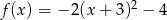 jest
jest
A) 3 B) -2 C) -4 D) 4
Największą wartością funkcji kwadratowej 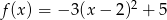 jest
jest
A) -3 B) 5 C) -5 D) 2
Liczba 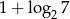 jest równa:
jest równa:
A) 3 B) 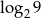 C) 4,5 D)
C) 4,5 D) 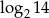
Liczba o 2 większa od liczby 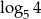 jest równa
jest równa
A) 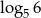 B)
B) 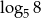 C)
C) 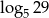 D)
D) 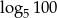
Liczba o 3 większa od 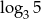 jest równa
jest równa
A) 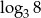 B)
B) 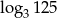 C)
C) 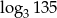 D)
D) 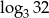
Liczba 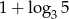 jest równa:
jest równa:
A) 2 B) 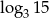 C)
C) 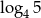 D)
D) 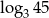
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 37035 B) 13629 C) 17023 D) 26919
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 67035 B) 49629 C) 17022 D) 16919
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 5,55 zł. Cena tego towaru bez podatku VAT jest równa
A) 37 zł B) 39,59 zł C) 42,55 zł D) 25,23 zł
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 6,45 zł. Cena tego towaru przed wprowadzeniem podatku VAT była równa
A) 5,48 zł B) 43 zł C) 49,45 zł D) 96,75 zł
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 10,65 zł. Cena tego towaru przed wprowadzeniem podatku VAT była równa
A) 92,61 zł B) 12,25 zł C) 71 zł D) 81,65 zł
Funkcja 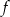 określona jest wzorem
określona jest wzorem 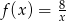 . Zbiór
. Zbiór 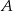 jest zbiorem wszystkich liczb całkowitych
jest zbiorem wszystkich liczb całkowitych  takich, że
takich, że 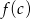 jest liczbą całkowitą. Zatem liczba elementów zbioru
jest liczbą całkowitą. Zatem liczba elementów zbioru 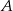 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Funkcja 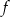 określona jest wzorem
określona jest wzorem 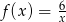 . Zbiór
. Zbiór 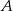 jest zbiorem wszystkich liczb całkowitych
jest zbiorem wszystkich liczb całkowitych  takich, że
takich, że 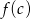 jest liczbą całkowitą. Zatem liczba elementów zbioru
jest liczbą całkowitą. Zatem liczba elementów zbioru 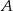 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Liczba 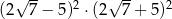 jest równa
jest równa
A) 9 B) 3 C) 2809 D) 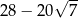
Liczba 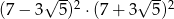 jest równa
jest równa
A) 49 B) 376 C) 16 D)