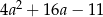Odległość między środkami okręgów o równaniach 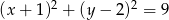 oraz
oraz 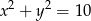 jest równa
jest równa
A) 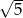 B)
B) 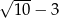 C) 3 D) 5
C) 3 D) 5
/Szkoła średnia/Zadania testowe
Odległość między środkami okręgów o równaniach 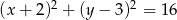 oraz
oraz 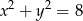 jest równa
jest równa
A) 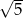 B)
B) 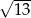 C) 13 D)
C) 13 D) 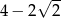
Odległość między środkami okręgów o równaniach 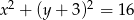 oraz
oraz 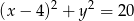 jest równa
jest równa
A) 3 B) 4 C) 5 D) 25
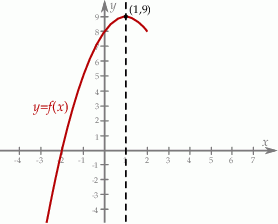
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 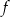 , określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty
, określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty 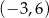 i
i 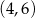 , a liczba
, a liczba 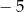 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 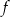 .
.
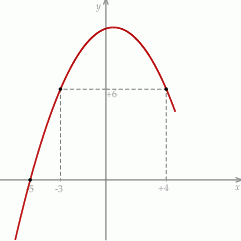
Drugim miejscem zerowym funkcji 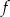 jest liczba
jest liczba
A) 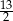 B) 6 C)
B) 6 C) 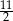 D) 5
D) 5
Pole trójkąta o bokach 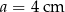 i
i 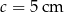 oraz kącie
oraz kącie 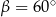 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 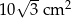 B)
B) 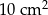 C)
C) 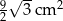 D)
D) 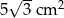
Ile wynosi pole trójkąta, w którym dwa boki mają długości 7 i 12, a kąt zawarty między nimi wynosi 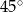 ?
?
A) 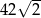 B) 42 C)
B) 42 C) 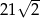 D) 21
D) 21
Pole trójkąta o bokach długości 4 oraz 9 i kącie między nimi o mierze 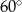 jest równe
jest równe
A) 18 B) 9 C) 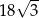 D)
D) 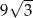
Pole trójkąta o bokach 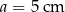 i
i 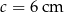 oraz kącie
oraz kącie 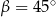 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 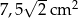 B)
B) 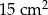 C)
C) 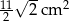 D)
D) 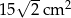
Dany jest trójkąt 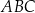 , w którym
, w którym 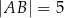 ,
, 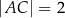 oraz
oraz 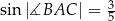 . Pole trójkąta
. Pole trójkąta 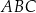 jest równe
jest równe
A) 3 B) 5 C) 6 D) 10
Długości boków trójkąta wynoszą 2 i 8, zaś kąt między nimi zawarty ma miarę 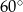 . Pole tego trójkąta wynosi
. Pole tego trójkąta wynosi
A) 8 B) 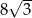 C) 4 D)
C) 4 D) 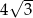
Prosta o równaniu 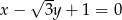 jest nachylona do osi
jest nachylona do osi 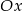 pod kątem
pod kątem  . Zatem
. Zatem
A) 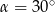 B)
B) 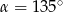 C)
C) 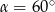 D)
D) 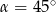
Prosta k o równaniu 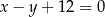 , tworzy z osią
, tworzy z osią 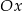 kąt o mierze równej
kąt o mierze równej
A) 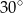 B)
B) 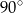 C)
C) 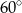 D)
D) 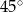
Prosta o równaniu 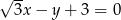 jest nachylona do osi
jest nachylona do osi 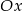 pod kątem
pod kątem  . Zatem
. Zatem
A) 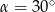 B)
B) 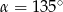 C)
C) 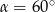 D)
D) 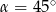
Prosta o równaniu 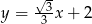 jest nachylona do osi
jest nachylona do osi 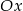 pod kątem
pod kątem  , takim, że
, takim, że
A) 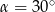 B)
B) 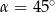 C)
C) 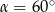 D)
D) 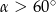
Prosta o równaniu 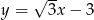 jest nachylona do osi
jest nachylona do osi 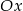 pod kątem
pod kątem
A) 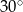 B)
B) 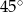 C)
C) 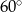 D)
D) 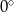
Wybieramy liczbę  ze zbioru
ze zbioru 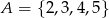 oraz liczbę
oraz liczbę 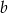 ze zbioru
ze zbioru 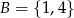 . Ile jest takich par
. Ile jest takich par 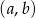 , że iloczyn
, że iloczyn 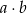 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 5 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 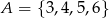 oraz liczbę
oraz liczbę 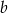 ze zbioru
ze zbioru 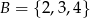 . Ile jest takich par
. Ile jest takich par 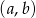 , że iloczyn
, że iloczyn 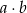 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 12 B) 3 C) 2 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 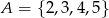 oraz liczbę
oraz liczbę 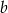 ze zbioru
ze zbioru 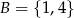 . Ile jest takich par
. Ile jest takich par 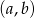 , że iloczyn
, że iloczyn 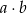 jest liczbą parzystą?
jest liczbą parzystą?
A) 2 B) 8 C) 6 D) 20
Wybieramy liczbę  ze zbioru
ze zbioru 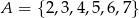 oraz liczbę
oraz liczbę 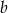 ze zbioru
ze zbioru 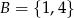 . Ile jest takich par
. Ile jest takich par 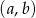 , że iloczyn
, że iloczyn 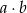 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 5 D) 20
Wartość wyrażenia 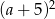 jest większa od wartości wyrażenia
jest większa od wartości wyrażenia 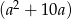 o
o
A) 50 B) 10 C) 5 D) 25
Wartość wyrażenia 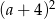 jest większa od wartości wyrażenia
jest większa od wartości wyrażenia 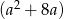 o
o
A) 4 B) 16 C) 64 D) 8
Objętość sześcianu, w którym przekątna ściany bocznej ma długość 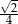 , jest równa
, jest równa
A) 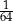 B)
B) 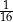 C) 16 D) 64
C) 16 D) 64
Przekątna ściany sześcianu ma długość 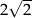 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 8 B) 24 C) 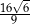 D)
D) 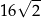
Jeżeli 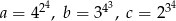 to
to
A) 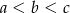 B)
B) 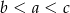 C)
C) 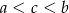 D)
D) 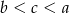
Wiadomo, że 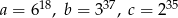 . Zatem
. Zatem
A) 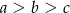 B)
B) 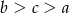 C)
C) 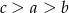 D)
D) 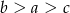
Wiadomo, że 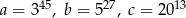 . Zatem
. Zatem
A) 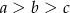 B)
B) 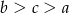 C)
C) 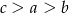 D)
D) 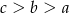
Wiadomo, że 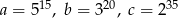 . Zatem
. Zatem
A) 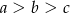 B)
B) 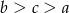 C)
C) 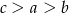 D)
D) 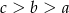
Liczba 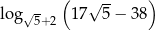 jest równa
jest równa
A) 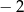 B)
B) 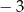 C)
C) 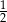 D)
D) 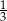
Dany jest zestaw danych: 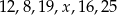 , gdzie
, gdzie  jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
A) 14 B) 17,5 C) 13,5 D) 16,5
Na podstawie fragmentu wykresu funkcji kwadratowej 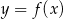 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
A) Miejscami zerowymi funkcji są liczby: 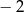 oraz 4.
oraz 4.
B) Funkcja jest rosnąca w przedziale 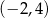 .
.
C) Funkcja przyjmuje wartości większe od zera dla 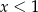 .
.
D) Zbiorem wartości funkcji jest przedział 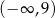 .
.
Na rysunku znajduje się fragment wykresu funkcji kwadratowej 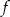 , określonej na zbiorze
, określonej na zbiorze 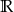 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
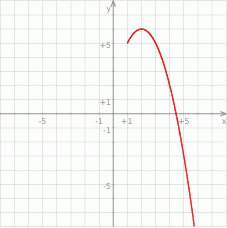
A) Wykres funkcji 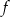 przecina oś
przecina oś 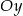 w punkcie
w punkcie 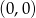 .
.
B) Dla argumentu 6 funkcja 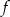 przyjmuje wartość 2.
przyjmuje wartość 2.
C) Funkcja jest rosnąca w przedziale 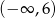 .
.
D) Funkcja 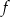 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 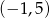 .
.
Na podstawie fragmentu wykresu funkcji kwadratowej 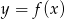 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
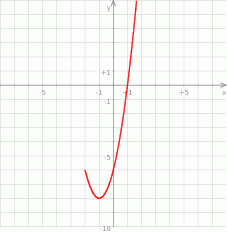
A) Jeżeli 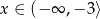 to
to 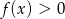 .
.
B) Do wykresu funkcji należy punkt 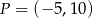 .
.
C) Wartości funkcji są dodatnie dla 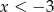 .
.
D) Miejscami zerowymi funkcji 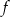 są liczby: 1 oraz -4.
są liczby: 1 oraz -4.
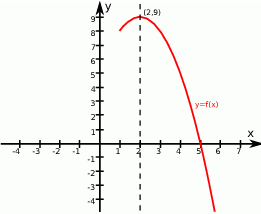
Na podstawie fragmentu wykresu funkcji kwadratowej 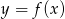 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
A) Funkcja jest rosnąca w przedziale 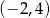 .
.
B) Miejscami zerowymi funkcji są liczby: -1 oraz 5.
C) Funkcja przyjmuje wartości dodatnie dla 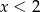 .
.
D) Zbiorem wartości funkcji jest przedział 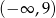 .
.
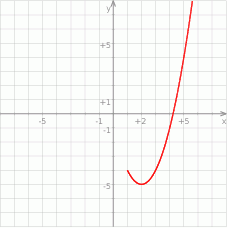
Na rysunku znajduje się fragment wykresu funkcji kwadratowej 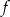 , określonej na zbiorze
, określonej na zbiorze 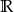 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Wykres funkcji 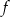 przecina oś
przecina oś 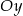 w punkcie
w punkcie 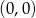 .
.
B) Dla argumentu 6 funkcja 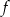 przyjmuje wartość 2.
przyjmuje wartość 2.
C) Funkcja jest malejąca w przedziale 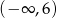 .
.
D) Funkcja 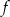 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 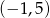 .
.
Na podstawie fragmentu wykresu funkcji kwadratowej 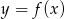 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe.
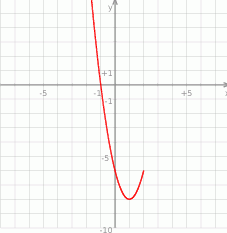
A) Jeżeli 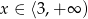 to
to 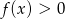 .
.
B) Do wykresu funkcji należy punkt 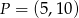 .
.
C) Miejscami zerowymi funkcji 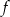 są liczby: -1 oraz 4.
są liczby: -1 oraz 4.
D) Wartości funkcji są dodatnie dla 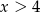 .
.
Na rysunku znajduje się fragment wykresu funkcji kwadratowej 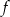 , określonej na zbiorze
, określonej na zbiorze 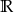 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
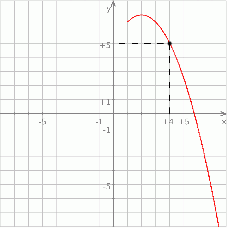
A) Wykres funkcji 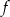 przecina oś
przecina oś 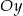 w punkcie
w punkcie 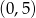 .
.
B) Dla argumentu 6 funkcja 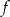 przyjmuje wartość 2.
przyjmuje wartość 2.
C) Funkcja jest rosnąca w przedziale 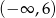 .
.
D) Funkcja 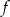 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 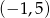 .
.
Na bokach 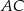 i
i 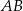 trójkąta
trójkąta 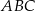 o wierzchołkach
o wierzchołkach 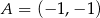 ,
, 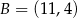 i
i 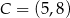 , wybrano punkty
, wybrano punkty 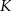 i
i 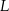 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 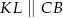 . Pole trapezu
. Pole trapezu 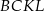 stanowi
stanowi 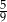 pola trójkąta
pola trójkąta 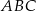 . Zatem
. Zatem
A) 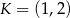 B)
B) 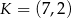 C)
C) 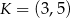 D)
D) 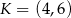
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 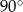 B)
B) 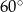 C)
C) 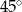 D)
D) 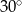
Podstawą ostrosłupa prawidłowego czworokątnego 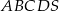 jest kwadrat
jest kwadrat 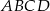 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 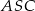 jest równa
jest równa
A) 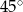 B)
B) 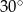 C)
C) 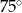 D)
D) 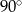
Podstawą ostrosłupa prawidłowego czworokątnego 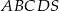 jest kwadrat
jest kwadrat 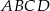 . Jaka jest miara kąta
. Jaka jest miara kąta 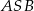 jeżeli trójkąt
jeżeli trójkąt 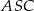 jest prostokątny?
jest prostokątny?
A) 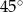 B)
B) 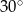 C)
C) 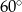 D)
D) 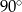
Podstawą ostrosłupa prawidłowego czworokątnego 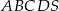 jest kwadrat
jest kwadrat 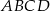 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 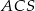 jest równa
jest równa
A) 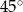 B)
B) 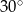 C)
C) 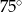 D)
D) 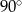
W ostrosłupie prawidłowym czworokątnym stosunek długości krawędzi bocznej do długości krawędzi podstawy wynosi 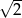 . Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 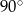 B)
B) 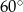 C)
C) 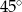 D)
D) 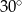
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 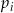 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 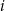 . Wtedy
. Wtedy
A) 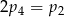 B)
B) 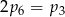 C)
C) 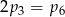 D)
D) 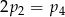
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 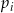 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 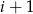 . Wtedy
. Wtedy
A) 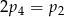 B)
B) 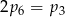 C)
C) 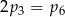 D)
D) 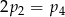
Dana jest funkcja 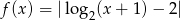 . Wykres tej funkcji jest przedstawiony na rysunku
. Wykres tej funkcji jest przedstawiony na rysunku
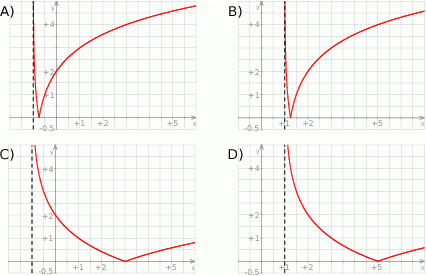
Wyrażenie 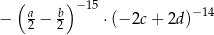 jest równe wyrażeniu
jest równe wyrażeniu
A) 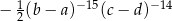 B)
B) 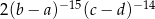
C) 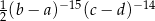 D)
D) 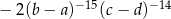
Po wymnożeniu wyrażeń 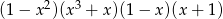 najwyższa potęga
najwyższa potęga  jaką otrzymamy to
jaką otrzymamy to
A) 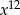 B)
B) 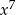 C)
C) 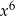 D)
D) 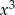
Po wymnożeniu wyrażeń 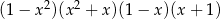 najwyższa potęga
najwyższa potęga  jaką otrzymamy to
jaką otrzymamy to
A) 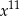 B)
B) 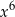 C)
C) 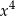 D)
D) 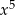
Po przekształceniu wyrażenia algebraicznego 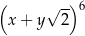 do postaci
do postaci
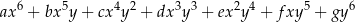
współczynnik 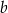 jest równy
jest równy
A) 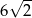 B) 6 C)
B) 6 C) 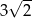 D) 12
D) 12
Punkt 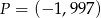 należy do wykresu funkcji
należy do wykresu funkcji 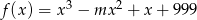 . Zatem
. Zatem
A) 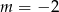 B)
B) 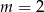 C)
C) 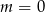 D)
D) 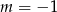
Punkt 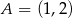 należy do wykresu funkcji
należy do wykresu funkcji 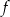 , określonej wzorem
, określonej wzorem
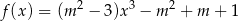
dla każdej liczby rzeczywistej  . Wtedy
. Wtedy
A) 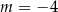 B)
B) 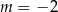 C)
C) 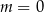 D)
D) 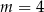
Punkt 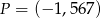 należy do wykresu funkcji
należy do wykresu funkcji 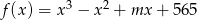 . Zatem
. Zatem
A) 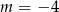 B)
B) 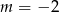 C)
C) 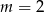 D)
D) 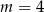
Wyrażenie 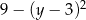 jest równe
jest równe
A) 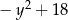 B)
B) 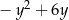 C)
C) 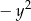 D)
D) 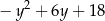
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 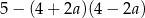 jest równe
jest równe
A) 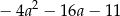 B)
B) 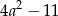 C)
C) 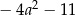 D)
D)