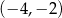Odcinek podzielono na dwie części w stosunku 1:3. Ile procent całego odcinka stanowi większa jego część?
A) 75% B) 25% C) 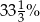 D)
D) 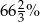
/Szkoła średnia/Zadania testowe
Cyfra jedności liczby 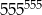 jest taka sama jak cyfra jedności liczby
jest taka sama jak cyfra jedności liczby
A) 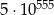 B)
B) 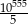 C)
C) 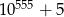 D)
D) 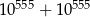
Cyfra jedności liczby 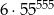 jest taka sama jak cyfra jedności liczby
jest taka sama jak cyfra jedności liczby
A) 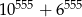 B)
B) 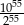 C)
C) 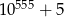 D)
D) 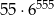
Cyfra jedności liczby 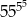 jest taka sama jak cyfra jedności liczby
jest taka sama jak cyfra jedności liczby
A) 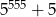 B)
B) 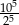 C)
C) 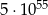 D)
D) 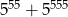
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 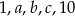 . Mediana liczb:
. Mediana liczb: 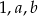 jest równa 3, a mediana liczb:
jest równa 3, a mediana liczb: 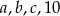 jest równa 5. Liczba
jest równa 5. Liczba  jest równa
jest równa
A) 4 B) 5 C) 6 D) 7
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 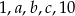 . Mediana liczb:
. Mediana liczb: 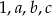 jest równa 3, a mediana liczb:
jest równa 3, a mediana liczb: 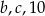 jest równa 8. Liczba
jest równa 8. Liczba 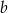 jest równa
jest równa
A) 4 B) 5 C) 6 D) 7
Dane jest równanie 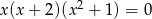 . Do zbioru rozwiązań tego równania należy liczba
. Do zbioru rozwiązań tego równania należy liczba
A) 2 B) 1 C) 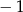 D) 0
D) 0
Który z czworokątów ma zawsze więcej niż dwie osie symetrii?
A) deltoid B) prostokąt C) kwadrat D) romb
Każdy bok trójkąta prostokątnego o bokach 3, 4, 5 kolorujemy jednym z 6 kolorów tak, aby żadne dwa boki nie były pokolorowane tym samym kolorem. Ile jest takich pokolorowań?
A) 15 B) 120 C) 216 D) 20
Punkty 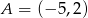 i
i 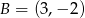 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 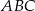 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 30 B) 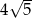 C)
C) 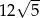 D) 36
D) 36
Punkty 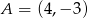 i
i 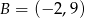 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 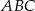 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 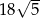 B)
B) 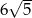 C) 45 D) 54
C) 45 D) 54
Punkty 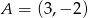 i
i 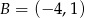 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 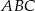 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 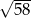 B)
B) 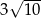 C)
C) 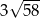 D)
D) 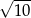
Punkty 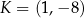 oraz
oraz 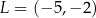 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 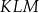 . Pole trójkąta
. Pole trójkąta 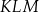 jest równe
jest równe
A) 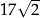 B)
B) 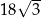 C)
C) 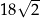 D)
D) 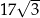
Punkty 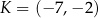 oraz
oraz 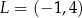 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego  . Pole trójkąta
. Pole trójkąta  jest równe
jest równe
A) 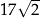 B)
B) 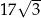 C)
C) 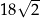 D)
D) 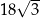
Wśród liczb naturalnych należących do przedziału (31, 41)
A) nie ma liczb pierwszych B) jest jedna liczba pierwsza
C) są dwie liczby pierwsze D) są trzy liczby pierwsze
Wśród liczb naturalnych należących do przedziału (21, 31)
A) nie ma liczb pierwszych B) jest jedna liczba pierwsza
C) są dwie liczby pierwsze D) są trzy liczby pierwsze
Wśród liczb naturalnych należących do przedziału (22, 32)
A) nie ma liczb pierwszych B) jest jedna liczba pierwsza
C) są dwie liczby pierwsze D) są trzy liczby pierwsze
Funkcje kwadratowe 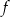 i
i 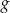 określone są wzorami
określone są wzorami 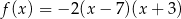 i
i 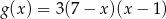 . Liczby
. Liczby 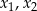 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 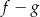 . Zatem
. Zatem
A) 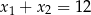 B)
B) 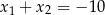 C)
C) 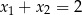 D)
D) 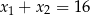
Ciąg 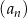 jes określony wzorem
jes określony wzorem 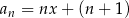 dla
dla 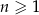 i pewnej liczby rzeczywistej
i pewnej liczby rzeczywistej  . Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy
. Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy  jest równe
jest równe
A) 3 B) 1,5 C) 27 D) 6
Iloczyn dodatnich liczb 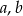 i
i  jest równy 6048. Ponadto 9% liczby
jest równy 6048. Ponadto 9% liczby  jest równe 8% liczby
jest równe 8% liczby 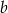 , oraz 70% liczby
, oraz 70% liczby 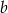 jest równe 60% liczby
jest równe 60% liczby  . Stąd wynika, że iloczyn
. Stąd wynika, że iloczyn 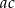 jest równy
jest równy
A) 288 B) 378 C) 324 D) 336
Funkcja 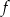 , określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie
, określona dla wszystkich liczb całkowitych dodatnich, przyporządkowuje liczbie  resztę z dzielenia tej liczby przez 7. Która z poniższych funkcji nie ma miejsca zerowego?
resztę z dzielenia tej liczby przez 7. Która z poniższych funkcji nie ma miejsca zerowego?
A) 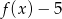 B)
B) 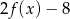 C)
C) 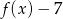 D)
D) 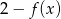
Dany jest sześcian 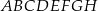 o krawędzi długości 9. Wierzchołki podstawy
o krawędzi długości 9. Wierzchołki podstawy 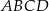 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem  , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
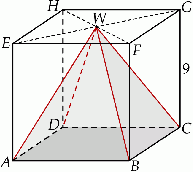
Objętość 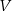 ostrosłupa
ostrosłupa 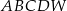 jest równa
jest równa
A) 243 B) 364,5 C) 489 D) 729
Dany jest sześcian 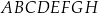 o krawędzi długości 6. Wierzchołki
o krawędzi długości 6. Wierzchołki 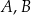 i
i 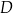 podstawy
podstawy 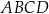 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 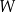 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 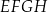 . Otrzymano w ten sposób ostrosłup trójkątny
. Otrzymano w ten sposób ostrosłup trójkątny  .
.
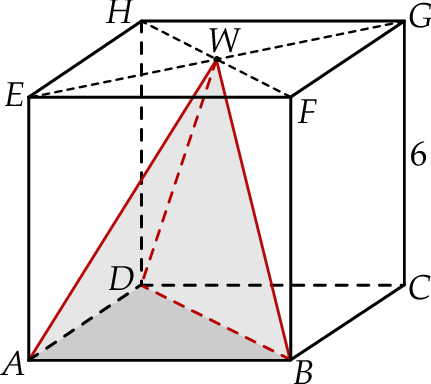
Objętość  ostrosłupa
ostrosłupa  jest równa
jest równa
A) 108 B) 72 C) 216 D) 36
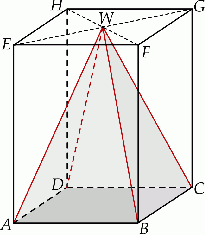
Dany jest graniastosłup prawidłowy czworokątny 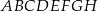 o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy
o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy 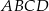 graniastosłupa połączono odcinkami z punktem
graniastosłupa połączono odcinkami z punktem 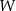 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 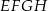 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny 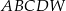 .
.
Objętość  ostrosłupa
ostrosłupa  jest równa
jest równa
A) 972 B) 162 C) 324 D) 243
Funkcja kwadratowa 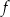 jest określona wzorem
jest określona wzorem 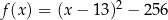 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 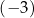 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 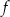 jest liczba
jest liczba
A) 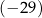 B)
B) 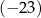 C) 23 D) 29
C) 23 D) 29
Funkcja kwadratowa 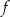 jest określona wzorem
jest określona wzorem 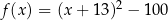 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 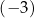 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 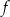 jest liczba
jest liczba
A) 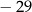 B)
B) 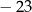 C) 23 D) 29
C) 23 D) 29
Do okręgu o środku 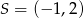 i promieniu
i promieniu 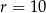 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 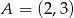 B)
B) 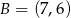 C)
C) 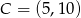 D)
D) 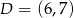
Dany jest okrąg o środku 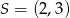 i promieniu
i promieniu 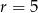 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 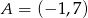 B)
B) 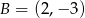 C)
C) 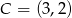 D)
D) 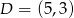
Dany jest okrąg o środku 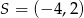 i promieniu
i promieniu 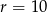 . Który z podanych punktów leży na tym okręgu?
. Który z podanych punktów leży na tym okręgu?
A) 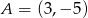 B)
B) 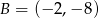 C)
C) 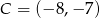 D)
D) 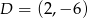
Do okręgu o środku 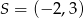 i promieniu
i promieniu 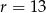 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 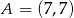 B)
B) 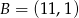 C)
C) 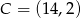 D)
D) 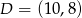
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najmniej jedną ścianę?
A) 37 B) 56 C) 60 D) 63
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najwyżej jedną ścianę.?
A) 48 B) 56 C) 40 D) 32
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najmniej dwie ściany?
A) 32 B) 72 C) 56 D) 40
Dana jest funkcja liniowa 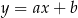 , o której wiadomo, że
, o której wiadomo, że 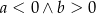 . Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
. Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
A) I, II, III B) I, II, IV C) II, III, IV D) I, III, IV
Dana jest funkcja liniowa 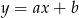 , o której wiadomo, że
, o której wiadomo, że 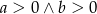 . Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
. Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
A) I, II, III B) I, II, IV C) II, III, IV D) I, III, IV
Dana jest funkcja liniowa 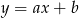 , o której wiadomo, że
, o której wiadomo, że 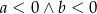 . Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
. Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
A) I, II, III B) I, II, IV C) II, III, IV D) I, III, IV
Która z poniższych funkcji, określonych w zbiorze liczb rzeczywistych, nie ma minimum lokalnego ani maksimum lokalnego?
A) 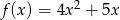 B)
B) 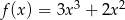 C)
C) 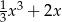 D)
D) 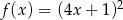
Która z poniższych funkcji, określonych w zbiorze liczb rzeczywistych, nie ma minimum lokalnego ani maksimum lokalnego?
A) 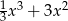 B)
B) 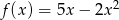 C)
C) 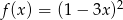 D)
D) 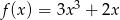
Trapez równoramienny  jest wpisany w okrąg o środku
jest wpisany w okrąg o środku  (zobacz rysunek).
(zobacz rysunek).
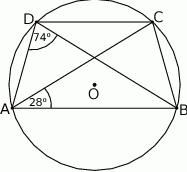
Różnica miar kątów 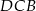 i
i 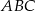 tego trapezu jest równa
tego trapezu jest równa
A) 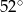 B)
B) 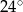 C)
C) 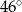 D)
D) 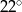
Jeśli 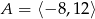 i
i 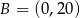 , to różnica
, to różnica 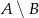 jest przedziałem
jest przedziałem
A) 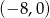 B)
B) 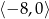 C)
C) 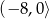 D)
D) 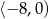
Różnicą przedziałów 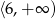 i
i 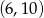 jest
jest
A) 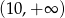 B)
B) 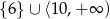 C)
C) 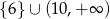 D)
D) 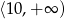
Jeśli 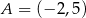 i
i 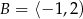 , to różnica przedziałów
, to różnica przedziałów 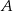 i
i 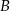 jest równa
jest równa
A) 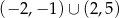 B)
B) 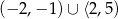 C)
C) 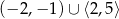 D)
D) 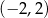
Jeśli 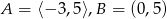 , to różnica
, to różnica 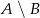 jest zbiorem
jest zbiorem
A) 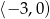 B)
B) 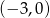 C)
C) 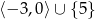 D)
D) 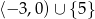
Dane są zbiory 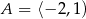 oraz
oraz 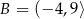 . Różnica
. Różnica 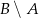 jest równa
jest równa
A) 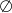 B)
B) 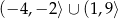 C)
C) 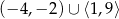 D)
D)