Wskaż liczbę, która spełnia równanie 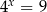 .
.
A) 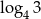 B)
B) 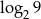 C)
C) 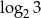 D)
D) 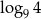
/Szkoła średnia/Zadania testowe
Jeśli 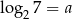 , to liczba
, to liczba 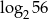 jest równa
jest równa
A) 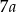 B)
B) 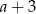 C)
C) 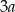 D)
D) 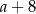
Jeżeli 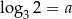 , to liczba
, to liczba 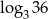 jest równa
jest równa
A) 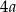 B)
B) 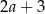 C)
C) 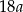 D)
D) 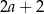
Jeśli 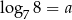 , to liczba
, to liczba 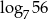 jest równa
jest równa
A) 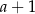 B)
B) 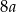 C)
C) 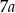 D)
D) 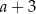
Jeśli 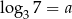 , to liczba
, to liczba 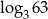 jest równa
jest równa
A) 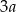 B)
B) 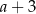 C)
C) 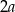 D)
D) 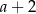
Wiedząc, że 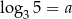 , określ wartość wyrażenia
, określ wartość wyrażenia 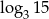 jest równa
jest równa
A) 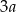 B)
B) 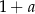 C)
C) 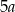 D)
D) 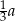
Niech 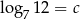 . Wtedy
. Wtedy 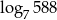 jest równy
jest równy
A) 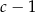 B)
B)  C)
C) 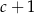 D)
D) 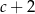
Niech 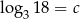 . Wtedy
. Wtedy 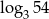 jest równy
jest równy
A) 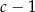 B)
B)  C)
C) 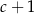 D)
D) 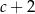
Liczba 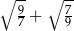 jest równa
jest równa
A) 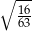 B)
B) 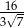 C) 1 D)
C) 1 D) 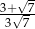
Liczba 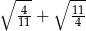 jest równa
jest równa
A) 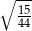 B)
B) 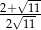 C) 1 D)
C) 1 D) 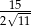
Wysokość w trójkącie prostokątnym dzieli podstawę na odcinki o długościach 3 i 5. Pole tego trójkąta jest równe:
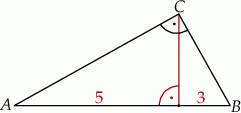
A) 15 B) 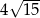 C) 16 D) za mało danych
C) 16 D) za mało danych
Podstawą ostrosłupa jest kwadrat 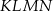 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 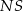 , a jej długość też jest równa 4 (zobacz rysunek).
, a jej długość też jest równa 4 (zobacz rysunek).
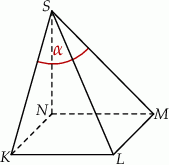
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 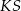 i
i 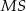 , spełnia warunek
, spełnia warunek
A) 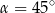 B)
B) 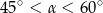 C)
C) 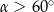 D)
D) 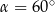
Prosta o równaniu 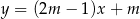 nie przecina prostej o równaniu
nie przecina prostej o równaniu 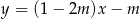 . Zatem
. Zatem
A) 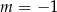 B)
B) 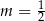 C)
C) 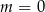 D)
D) 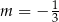
W ciągu geometrycznym 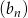 wyraz
wyraz 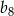 jest równy
jest równy 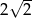 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 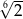 . Wobec tego
. Wobec tego
A) 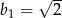 B)
B) 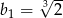 C)
C) 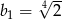 D)
D) 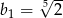
W ciągu geometrycznym 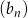 wyraz
wyraz 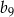 jest równy
jest równy 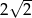 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 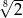 . Wobec tego
. Wobec tego
A) 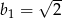 B)
B) 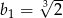 C)
C) 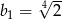 D)
D) 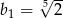
W ciągu geometrycznym 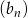 wyraz
wyraz 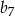 jest równy
jest równy 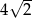 , zaś iloraz tego ciągu ma wartość
, zaś iloraz tego ciągu ma wartość 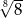 . Wobec tego
. Wobec tego
A) 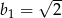 B)
B) 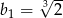 C)
C) 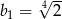 D)
D) 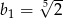
Pole równoległoboku 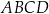 jest równe
jest równe 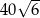 . Bok
. Bok 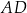 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 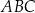 równoległoboku ma miarę
równoległoboku ma miarę 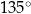 (zobacz rysunek).
(zobacz rysunek).

Długość boku 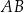 jest równa
jest równa
A) 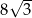 B)
B) 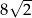 C)
C) 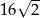 D)
D) 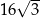
Pole równoległoboku 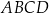 jest równe
jest równe 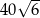 . Bok
. Bok 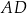 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 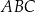 równoległoboku ma miarę
równoległoboku ma miarę 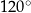 (zobacz rysunek).
(zobacz rysunek).

Długość boku 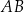 jest równa
jest równa
A) 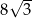 B)
B) 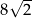 C)
C) 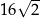 D)
D) 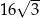
Liczby naturalne 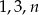 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 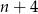 B)
B) 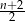 C)
C)  D) 3
D) 3
Liczby naturalne 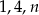 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 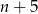 B)
B) 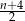 C) 4 D)
C) 4 D) 
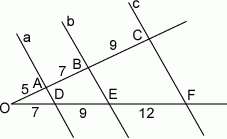
Proste 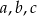 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 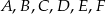 . Długości odcinków
. Długości odcinków 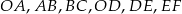 podane są na rysunku. Zatem
podane są na rysunku. Zatem
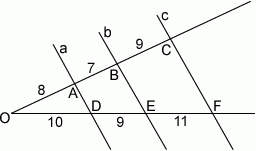
A)  B)
B)  C)
C)  D)
D) 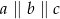
Proste 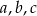 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 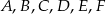 . Długość odcinków
. Długość odcinków 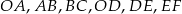 podane są na rysunku. Zatem
podane są na rysunku. Zatem
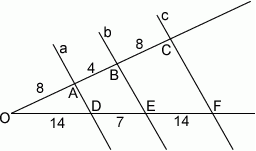
A)  B)
B)  C)
C)  D)
D) 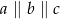
Proste 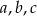 przecinają ramiona kąta odpowiednio w punktach
przecinają ramiona kąta odpowiednio w punktach 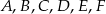 . Długość odcinków
. Długość odcinków 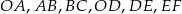 podane są na rysunku. Zatem
podane są na rysunku. Zatem
A) 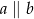 B)
B) 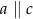 C)
C) 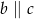 D)
D) 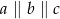
Prosta 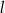 tworzy z osią
tworzy z osią 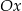 kąt
kąt 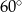 i przecina oś
i przecina oś 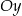 w punkcie
w punkcie 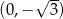 (zobacz rysunek).
(zobacz rysunek).
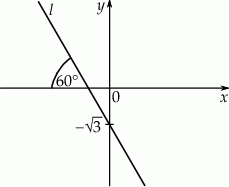
Prosta 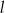 ma równanie
ma równanie
A) 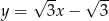 B)
B) 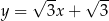 C)
C) 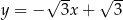 D)
D) 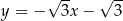
Prosta 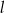 tworzy z osią
tworzy z osią 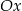 kąt ostry
kąt ostry 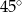 (zobacz rysunek) oraz przechodzi przez punkt o współrzędnych
(zobacz rysunek) oraz przechodzi przez punkt o współrzędnych 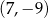 .
.
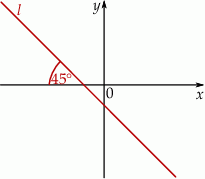
Prosta 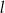 ma równanie
ma równanie
A) 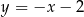 B)
B) 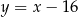 C)
C) 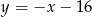 D)
D) 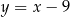
Liczba 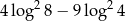 jest równa
jest równa
A) 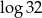 B)
B) 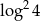 C)
C) 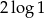 D)
D) 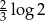
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 6, a jednym z jego kątów ostrych jest kąt 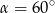 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 36 B) 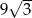 C) 18 D)
C) 18 D) 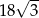
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 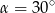 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 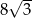 C) 8 D)
C) 8 D) 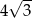
Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 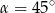 , to pole tego trójkąta jest równe
, to pole tego trójkąta jest równe
A) 16 B) 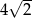 C) 8 D)
C) 8 D) 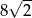
Do przedziału 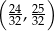 należy liczba
należy liczba
A) 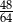 B)
B) 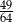 C)
C) 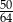 D)
D) 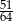
Do przedziału 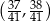 należy liczba
należy liczba
A) 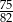 B)
B) 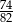 C)
C) 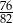 D)
D) 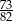
Do przedziału 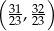 należy liczba
należy liczba
A) 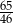 B)
B)  C)
C) 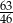 D)
D) 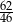
Punkt 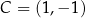 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 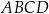 . Prosta o równaniu
. Prosta o równaniu 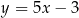 zawiera podstawę
zawiera podstawę 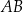 . Podstawa
. Podstawa 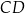 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 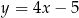 B)
B) 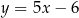 C)
C) 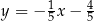 D)
D) 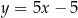
Dany jest trapez 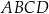 , w którym boki
, w którym boki 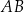 i
i 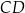 są równoległe oraz
są równoległe oraz 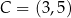 . Wierzchołki
. Wierzchołki 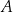 i
i 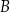 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 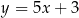 . Wtedy bok
. Wtedy bok 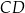 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 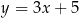 B)
B) 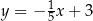 C)
C) 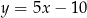 D)
D) 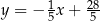
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 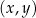 , dany jest trapez
, dany jest trapez 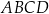 , w którym boki
, w którym boki 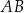 i
i 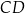 są równoległe oraz
są równoległe oraz 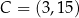 . Wierzchołki
. Wierzchołki 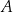 i
i 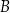 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 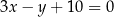 . Bok
. Bok 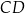 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 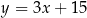 B)
B) 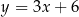 C)
C) 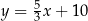 D)
D) 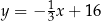
Punkt 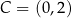 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 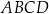 , którego podstawa
, którego podstawa 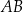 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 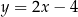 . Wskaż równanie prostej zawierającej podstawę
. Wskaż równanie prostej zawierającej podstawę 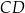 .
.
A) 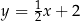 B)
B) 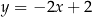 C)
C) 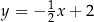 D)
D) 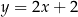
Punkt 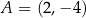 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 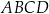 . Prosta o równaniu
. Prosta o równaniu 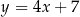 zawiera podstawę
zawiera podstawę 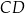 . Podstawa
. Podstawa 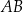 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 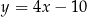 B)
B) 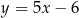 C)
C) 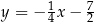 D)
D) 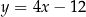
Jedna z przyprostokątnych trójkąta prostokątnego jest 3 razy dłuższa od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 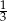 B) 3 C)
B) 3 C) 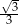 D)
D) 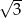
Przyprostokątne trójkąta prostokątnego mają długość 3 i 4. Wynika stąd, że tangens mniejszego z kątów ostrych jest równy
A)  B)
B)  C)
C) 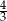 D)
D) 
W trójkącie prostokątnym o bokach 6, 8, 10, tangens najmniejszego kąta jest równy:
A)  B)
B) 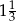 C)
C)  D)
D) 
Jedna z przyprostokątnych trójkąta prostokątnego jest 5 razy krótsza od drugiej. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 5 B) 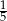 C)
C) 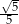 D)
D) 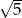
W ciągu geometrycznym 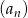 dane są:
dane są: 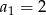 i
i 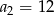 . Wtedy
. Wtedy
A) 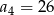 B)
B) 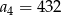 C)
C) 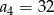 D)
D) 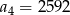
Jeżeli w ciągu geometrycznym 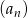 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 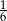 , a drugi wynosi
, a drugi wynosi 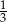 , to
, to
A) 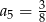 B)
B) 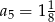 C)
C) 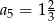 D)
D) 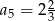
Jeżeli w ciągu geometrycznym 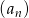 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 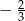 , a drugi wynosi 2, to
, a drugi wynosi 2, to
A) 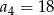 B)
B) 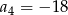 C)
C) 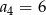 D)
D) 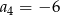
W ciągu geometrycznym 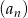 dane są:
dane są: 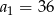 i
i 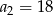 . Wtedy
. Wtedy
A) 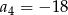 B)
B) 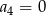 C)
C) 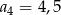 D)
D) 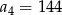
W ciągu geometrycznym 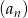 dane są:
dane są: 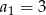 i
i 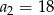 . Wtedy
. Wtedy
A) 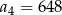 B)
B) 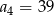 C)
C) 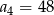 D)
D) 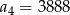
W ciągu geometrycznym 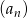 dane są:
dane są: 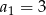 i
i 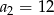 . Wtedy
. Wtedy
A) 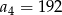 B)
B) 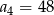 C)
C) 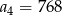 D)
D) 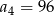
Dany jest okrąg o środku 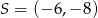 i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2014. Obrazem tego okręgu w symetrii osiowej względem osi 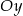 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 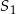 . Odległość między punktami
. Odległość między punktami 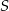 i
i 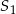 jest równa
jest równa
A) 12 B) 16 C) 2014 D) 4028
Dany jest okrąg o środku 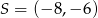 i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi 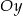 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 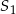 . Odległość między punktami
. Odległość między punktami 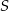 i
i 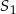 jest równa
jest równa
A) 12 B) 16 C) 2015 D) 4030
Ciąg 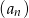 określony jest w następujący sposób
określony jest w następujący sposób 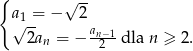 Setny wyraz ciągu
Setny wyraz ciągu 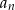 jest równy
jest równy
A) 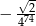 B)
B) 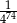 C)
C) 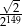 D)
D) 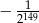
Wykresy funkcji 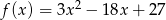 i
i 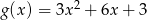 są symetryczne względem prostej
są symetryczne względem prostej
A) 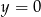 B)
B) 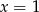 C)
C) 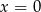 D)
D) 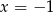
Wykresy funkcji 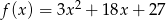 i
i 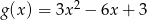 są symetryczne względem prostej
są symetryczne względem prostej
A) 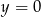 B)
B) 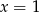 C)
C) 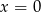 D)
D)