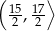Średnice 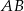 i
i 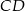 okręgu o środku
okręgu o środku 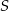 przecinają się pod kątem
przecinają się pod kątem 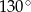 (tak jak na rysunku).
(tak jak na rysunku).
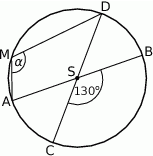
Miara kąta  jest równa
jest równa
A) 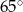 B)
B) 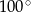 C)
C) 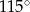 D)
D) 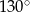
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Średnice 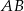 i
i 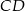 okręgu o środku
okręgu o środku 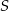 przecinają się pod kątem
przecinają się pod kątem 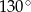 (tak jak na rysunku).
(tak jak na rysunku).

Miara kąta  jest równa
jest równa
A) 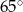 B)
B) 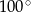 C)
C) 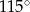 D)
D) 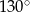
Punkty 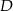 i
i 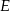 dzielą bok
dzielą bok 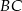 trójkąta
trójkąta 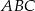 na trzy odcinki, których stosunek długości
na trzy odcinki, których stosunek długości 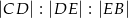 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 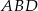 i
i 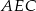 jest równy
jest równy
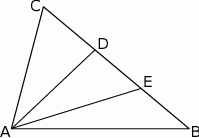
A)  B)
B) 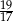 C)
C) 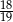 D)
D) 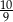
Jeżeli 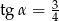 to to stosunek
to to stosunek 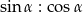 jest równy:
jest równy:
A) 4:3 B) 3:4 C) 1:1 D) 2:3
Jeżeli 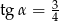 to to stosunek
to to stosunek 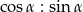 jest równy:
jest równy:
A) 4:3 B) 3:4 C) 1:1 D) 2:3
Która z podanych prostych nie przecina wykresu funkcji 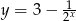 ?
?
A) 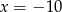 B)
B) 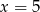 C)
C) 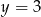 D)
D) 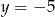
Dany jest sześcian 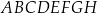 o krawędzi długości 5. Na przekątnej
o krawędzi długości 5. Na przekątnej 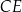 tego sześcianu znajduje się punkt
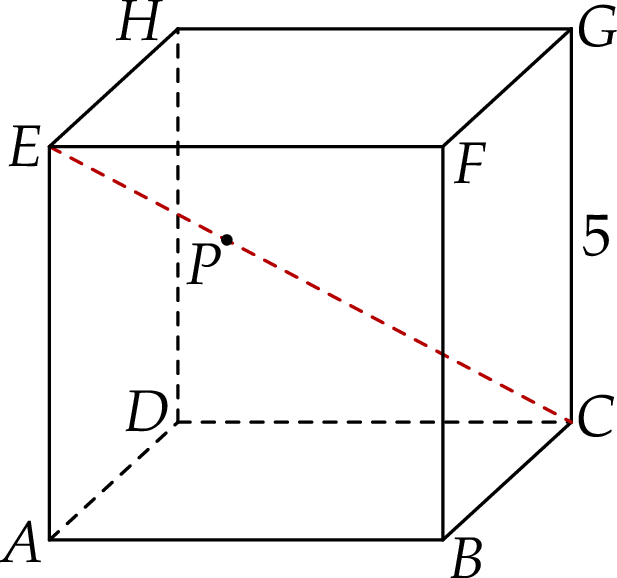
tego sześcianu znajduje się punkt 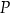 (zobacz rysunek).
(zobacz rysunek).
Suma odległości punktu 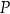 od krawędzi
od krawędzi 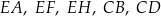 i
i 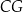 sześcianu
sześcianu 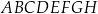 jest równa
jest równa
A) 15 B) 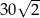 C)
C) 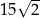 D) 30
D) 30
Parabola, która jest wykresem funkcji 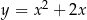 ma z prostą o równaniu
ma z prostą o równaniu 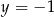
A) dwa punkty wspólne B) jeden punkt wspólny
C) zero punktów wspólnych D) trzy punkty wspólne
Liczba punktów wspólnych prostej 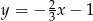 i paraboli
i paraboli 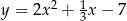 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Parabola, która jest wykresem funkcji 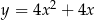 ma z prostą o równaniu
ma z prostą o równaniu 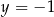
A) dwa punkty wspólne B) zero punktów wspólnych
C) jeden punkt wspólny D) trzy punkty wspólne
Do sklepu dostarczono  puszek napoju gazowanego o pojemności
puszek napoju gazowanego o pojemności 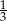 litra oraz
litra oraz 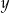 puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
A) 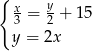 B)
B) 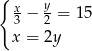 C)
C) 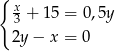 D)
D) 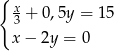
Właściciel sklepu kupił w hurtowni 12 identycznych wiertarek po  zł za sztukę i 15 identycznych szlifierek kątowych po
zł za sztukę i 15 identycznych szlifierek kątowych po 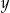 zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki
zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki  i szlifierki
i szlifierki 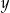 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 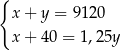 B)
B) 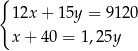
C) 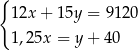 D)
D) 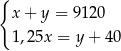
Pięć lat temu ojciec był 3 razy starszy od syna, a za 10 lat będą mieli w sumie 90 lat. Który układ równań opisuje tę sytuację?
A) 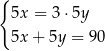 B)
B) 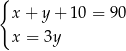
C) 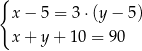 D)
D) 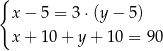
Właściciel sklepu kupił w hurtowni 50 par identycznych spodni po  zł za parę i 40 identycznych marynarek po
zł za parę i 40 identycznych marynarek po 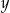 zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni
zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni  oraz cenę marynarki
oraz cenę marynarki 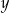 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 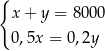 B)
B) 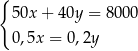 C)
C) 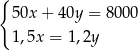 D)
D) 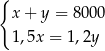
Do sklepu dostarczono  kubłów z farbą o pojemności 10 litrów oraz
kubłów z farbą o pojemności 10 litrów oraz 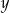 puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
A) 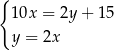 B)
B) 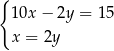
C) 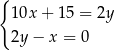 D)
D) 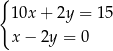
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew. Po roku stwierdzono, że uschło 5% drzew w pierwszym sadzie i 10% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła 60% liczby drzew, które pozostały w pierwszym sadzie. Niech  oraz
oraz 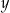 oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby
oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby  drzew posadzonych w pierwszym sadzie oraz liczby
drzew posadzonych w pierwszym sadzie oraz liczby 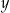 drzew posadzonych w drugim sadzie, jest
drzew posadzonych w drugim sadzie, jest
A) 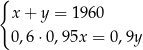 B)
B) 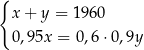
C) 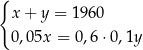 D)
D) 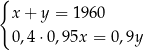
Poparcie społeczne dla partii „Zielone żabki” w marcu było równe 25%, a w kwietniu 20%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie społeczne dla partii „Radosna przyszłość” w marcu było równe 20%, a w kwietniu 15%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 27%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 25% D) 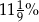
Poparcie społeczne dla partii „Radość i słońce” w marcu było równe 15%, a w kwietniu 12%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 20% B) 6% C) 3% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 40%. W kwietniu poparcie dla tej partii wynosiło 34%. Zatem poparcie dla partii "WESELI" zmalało o
A) 6% B) 12,5% C) 15% D) 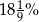
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 30%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 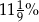 D) 25%
D) 25%
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 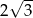 B)
B) 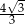 C)
C) 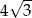 D) 6
D) 6
W trójkącie równobocznym wysokość jest równa 12. Zatem bok tego trójkąta ma długość
A) 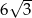 B)
B) 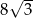 C) 24 D) 8
C) 24 D) 8
Jeżeli wysokość trójkąta równobocznego wynosi 3, to długość jego boku jest równa
A) 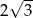 B)
B) 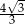 C)
C) 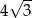 D) 6
D) 6
Jeżeli wysokość trójkąta równobocznego wynosi 6, to długość jego boku jest równa
A) 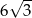 B)
B) 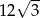 C)
C) 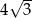 D) 18
D) 18
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 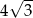 B)
B) 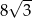 C)
C) 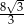 D) 12
D) 12
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 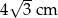 B) 12 cm C)
B) 12 cm C) 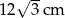 D)
D) 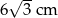
Jeśli 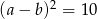 oraz
oraz 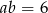 , to
, to 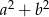 jest równe
jest równe
A) 18 B) 22 C) 20 D) 16
Jeśli 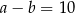 oraz
oraz 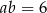 , to
, to 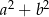 jest równe
jest równe
A) 122 B) 106 C) 94 D) 112
Średnia arytmetyczna dziesięciu liczb naturalnych: 3, 10, 5,  ,
,  ,
,  ,
,  , 12, 19, 7 jest równa 12. Mediana tych liczb jest równa
, 12, 19, 7 jest równa 12. Mediana tych liczb jest równa
A) 14 B) 12 C) 16 D) 
Średnia arytmetyczna zestawu danych: 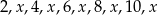 jest równa 4,5. Mediana tego zestawu danych wynosi
jest równa 4,5. Mediana tego zestawu danych wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Średnia arytmetyczna dziesięciu liczb naturalnych: 21, 11, 5,  ,
,  ,
,  ,
,  , 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
, 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
A) 11 B) 9 C) 10 D) 
Wartość wyrażenia 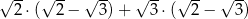 jest równa
jest równa
A) 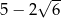 B) 5 C)
B) 5 C) 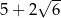 D)
D) 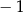
Wartość wyrażenia 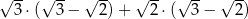 jest równa
jest równa
A) 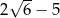 B) 1 C)
B) 1 C) 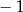 D)
D) 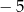
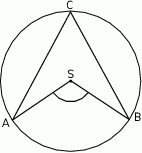
Punkt 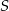 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 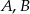 i
i 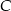 (patrz rysunek). Jeśli
(patrz rysunek). Jeśli 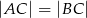 i miara kąta wypukłego
i miara kąta wypukłego 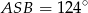 , to kąt wypukły
, to kąt wypukły 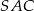 jest równy
jest równy
A) 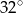 B)
B) 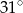 C)
C) 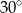 D)
D) 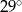
W trapezie miary kątów ostrych są równe 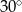 i
i 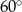 . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A) 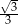 B)
B) 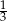 C)
C) 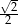 D)
D) 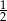
Czterowyrazowy ciąg 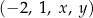 jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa
A) 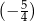 B)
B) 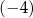 C)
C) 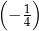 D)
D) 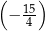
Układ równań 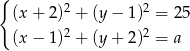 z niewiadomymi
z niewiadomymi 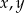 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 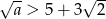 B)
B) 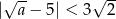 C)
C) 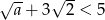 D)
D) 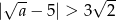
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 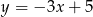 jest równy
jest równy
A) 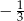 B) -3 C)
B) -3 C) 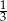 D) 3
D) 3
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 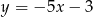 jest równy
jest równy
A) 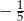 B) 5 C)
B) 5 C) 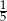 D) -5
D) -5
Dane są trzy okręgi o środkach 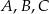 i promieniach równych odpowiednio
i promieniach równych odpowiednio 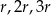 . Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli
. Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli 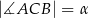 zaś
zaś 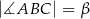 , to
, to
A) 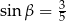 B)
B)  C)
C) 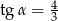 D)
D) 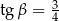
Jeżeli 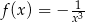 , to
, to
A) 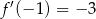 B)
B) 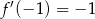 C)
C) 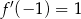 D)
D) 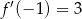
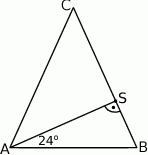
W trójkącie równoramiennym 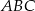 poprowadzono wysokość
poprowadzono wysokość 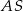 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 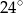 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 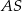 jest liczbą z przedziału
jest liczbą z przedziału
A) 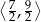 B)
B) 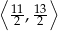 C)
C) 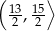 D)
D)