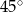Pole powierzchni równoległoboku jest równe 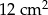 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 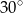 . Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
. Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
/Szkoła średnia/Zadania testowe
Pole powierzchni równoległoboku jest równe 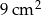 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 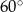 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 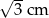 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole powierzchni równoległoboku jest równe 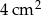 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 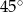 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 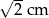 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Ile jest liczb naturalnych dwudziestocyfrowych, których iloczyn cyfr jest równy 25?
A) 380 B) 190 C) 250 D) 500
Rozwiązaniem nierówności 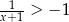 jest zbiór
jest zbiór
A) 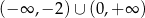 B)
B) 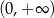
C) 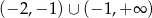 D)
D) 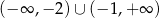
Rozwiązaniem nierówności 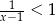 jest zbiór
jest zbiór
A) 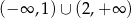 B)
B) 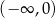
C) 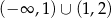 D)
D) 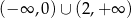
Równanie 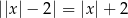
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Równanie 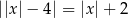
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie cztery rozwiązania.
Pole czworokąta przedstawionego na rysunku jest równe
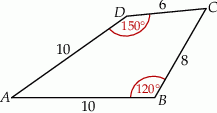
A) 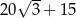 B)
B) 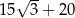 C)
C) 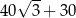 D)
D) 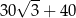
Latawiec leci na wysokości 8 m nad ziemią. Z punktu 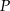 widać latawiec pod kątem
widać latawiec pod kątem  do poziomu. W jakiej odległości od punktu
do poziomu. W jakiej odległości od punktu 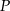 znajduje się latawiec?
znajduje się latawiec?
A) ![8 sin α [m ]](https://img.zadania.info/zad/5548319/HzadT3x.gif) B)
B) ![-8--[m ] sinα](https://img.zadania.info/zad/5548319/HzadT4x.gif) C)
C) ![sin-α 8 [m ]](https://img.zadania.info/zad/5548319/HzadT5x.gif) D)
D) ![-8- tg α [m ]](https://img.zadania.info/zad/5548319/HzadT6x.gif)
Balon leci na wysokości 12 m nad ziemią. Z punktu  widać latawiec pod kątem
widać latawiec pod kątem  do poziomu. W jakiej odległości od punktu
do poziomu. W jakiej odległości od punktu  znajduje się latawiec?
znajduje się latawiec?
A) ![12 sin α [m ]](https://img.zadania.info/zad/4155277/HzadT3x.gif) B)
B) ![sinα-[m ] 12](https://img.zadania.info/zad/4155277/HzadT4x.gif) C)
C) ![-12- sin α [m ]](https://img.zadania.info/zad/4155277/HzadT5x.gif) D)
D) ![12- tg α [m ]](https://img.zadania.info/zad/4155277/HzadT6x.gif)
Funkcja kwadratowa określona jest wzorem 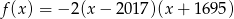 . Wynika stąd, że
. Wynika stąd, że
A) 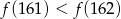 B)
B) 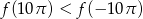 C)
C) 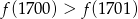 D)
D) 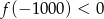
Przed podwyżką cena paczki gum i batonika była taka sama. Cenę paczki gum podniesiono o 10%, a za batonik trzeba zapłacić o 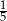 więcej. Zatem za trzy batoniki i dwie paczki gum trzeba teraz zapłacić więcej o
więcej. Zatem za trzy batoniki i dwie paczki gum trzeba teraz zapłacić więcej o
A) 32% B) 64% C) 16% D) 48%
Przed podwyżką cena pączka i drożdżówki była taka sama. Cenę pączka podniesiono o 20%, a za drożdżówkę trzeba zapłacić o 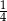 więcej. Zatem za cztery drożdżówki i sześć pączków trzeba teraz zapłacić więcej o
więcej. Zatem za cztery drożdżówki i sześć pączków trzeba teraz zapłacić więcej o
A) 20% B) 22% C) 25% D) 23%
Przed podwyżką ceny ołówka i długopisu były takie same. Cenę ołówka podniesiono o 25%, a za długopis trzeba zapłacić o 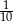 więcej. Zatem za cztery ołówki i jeden długopis trzeba teraz zapłacić więcej o
więcej. Zatem za cztery ołówki i jeden długopis trzeba teraz zapłacić więcej o
A) 20% B) 17,5% C) 13% D) 22%
Przed podwyżką ceny kwiatka i doniczki były takie same. Cenę doniczki podniesiono o 15%, a za kwiatka trzeba zapłacić o 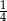 więcej. Zatem za dwa kwiatki i trzy doniczki trzeba teraz zapłacić więcej o
więcej. Zatem za dwa kwiatki i trzy doniczki trzeba teraz zapłacić więcej o
A) 19% B) 95% C) 21% D) 20%
Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii?
A) 25 B) 40 C) 45 D) 55
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Wielomian 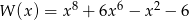 jest równy iloczynowi
jest równy iloczynowi
A) 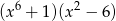 B)
B) 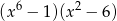 C)
C) 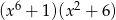 D)
D) 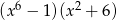
Na rysunku 1 jest przedstawiony wykres funkcji 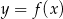 .
.
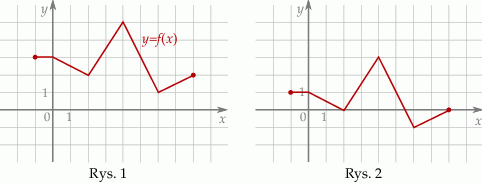
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 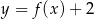 B)
B) 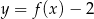 C)
C) 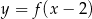 D)
D) 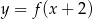
Na poniższych rysunkach przedstawiono wykresy funkcji 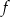 i
i 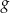 .
.
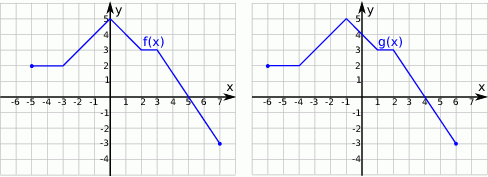
Funkcja  jest określona wzorem
jest określona wzorem
A)  B)
B)  C)
C) 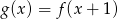 D)
D) 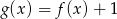
Na poniższych rysunkach przedstawiono wykresy funkcji 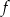 i
i 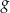 .
.
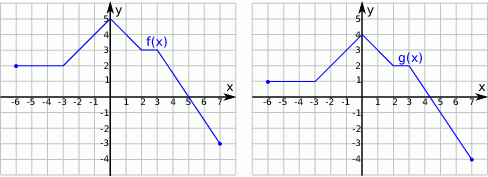
Funkcja  jest określona wzorem
jest określona wzorem
A)  B)
B)  C)
C) 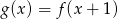 D)
D) 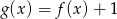
Na rysunku 1 jest przedstawiony wykres funkcji 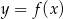 .
.
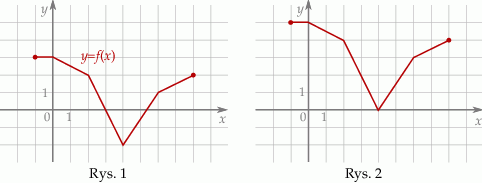
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 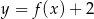 B)
B) 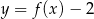 C)
C) 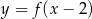 D)
D) 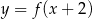
Styczna do wykresu funkcji 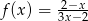 w punkcie o współrzędnych
w punkcie o współrzędnych 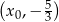 ma równanie
ma równanie
A) 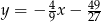 B)
B) 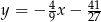 C)
C) 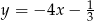 D)
D) 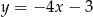
Wszystkie liczby spełniające warunek 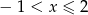 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 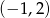 B)
B) 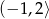 C)
C) 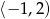 D)
D) 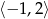
Wszystkie liczby spełniające warunek 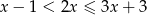 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 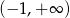 B)
B) 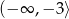 C)
C) 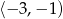 D)
D) 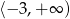
Zbiorem rozwiązań nierówności liniowej 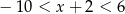 jest przedział liczbowy
jest przedział liczbowy
A) 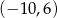 B)
B) 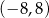 C)
C) 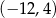 D)
D) 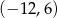
Trapez  , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu  . Pole trapezu
. Pole trapezu  jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 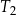 jest równy
jest równy
A) 18 B) 9 C) 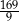 D)
D) 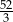
Wierzchołek paraboli 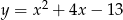 leży na prostej o równaniu
leży na prostej o równaniu
A) 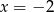 B)
B) 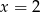 C)
C) 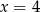 D)
D) 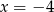
Wierzchołek paraboli 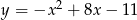 leży na prostej o równaniu
leży na prostej o równaniu
A) 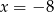 B)
B) 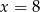 C)
C) 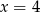 D)
D) 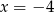
Wierzchołek paraboli 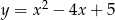 leży na prostej o równaniu
leży na prostej o równaniu
A) 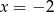 B)
B) 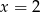 C)
C) 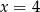 D)
D) 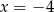
Wykresem funkcji kwadratowej 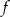 jest parabola o wierzchołku
jest parabola o wierzchołku 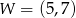 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 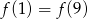 B)
B) 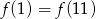 C)
C) 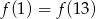 D)
D) 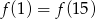
Wykresem funkcji kwadratowej 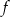 jest parabola o wierzchołku
jest parabola o wierzchołku 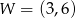 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 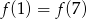 B)
B) 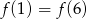 C)
C) 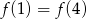 D)
D) 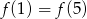
Wykresem funkcji kwadratowej 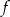 jest parabola o wierzchołku
jest parabola o wierzchołku 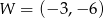 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 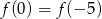 B)
B) 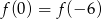 C)
C) 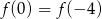 D)
D) 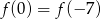
Wykresem funkcji kwadratowej 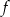 jest parabola o wierzchołku
jest parabola o wierzchołku 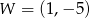 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 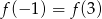 B)
B) 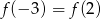 C)
C) 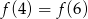 D)
D) 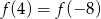
Do kwadratu pewnej liczby rzeczywistej dodano pięciokrotność tej liczby. Która z podanych liczb nie może być wynikiem takiego działania?
A) 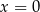 B)
B) 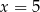 C)
C) 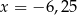 D)
D) 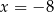
Kula ma objętość 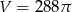 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Kula ma objętość 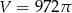 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Promień kuli o objętości 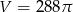 jest równy
jest równy
A) 18 B) 9 C) 8 D) 6
Równanie prostej przechodzącej przez punkty 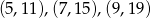 to
to
A) 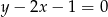 B)
B) 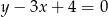 C)
C) 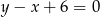 D)
D) 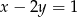
Czworokąt 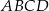 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 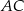 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 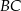 i
i 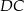 , a kąt
, a kąt 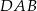 ma miarę
ma miarę 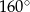 .
.
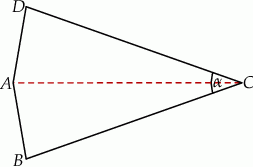
Miara kąta 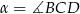 jest równa
jest równa
A) 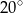 B)
B) 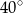 C)
C) 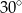 D)
D)