Zadanie nr 1479096
Funkcja 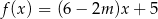 jest rosnąca wtedy i tylko wtedy, gdy
jest rosnąca wtedy i tylko wtedy, gdy
A) 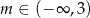 B)
B) 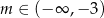 C)
C) 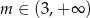 D)
D) 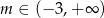
Rozwiązanie
Sposób I
Funkcja liniowa jest rosnąca jeżeli ma dodatni współczynnik kierunkowy (współczynnik przy  ), czyli
), czyli
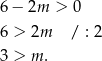
Sposób II
Przypomnijmy, że funkcja jest rosnąca jeżeli dla dowolnych 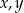 należących do dziedziny funkcji takich, że
należących do dziedziny funkcji takich, że 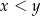 wartość funkcji w
wartość funkcji w  jest większa niż wartość funkcji w
jest większa niż wartość funkcji w 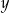 . Ustalmy dowolne
. Ustalmy dowolne  takie, że
takie, że 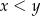 . Liczymy
. Liczymy
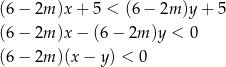
Ponieważ 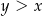 , więc
, więc 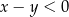 . Zatem aby nierówność była spełniona
. Zatem aby nierówność była spełniona 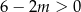 , czyli
, czyli 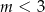
Odpowiedź: A

