/Szkoła średnia/Zadania testowe

Zadanie nr 1540968

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma rozwiązań równania 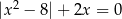2 |x − 8 |+ 2x = 0 jest równa
A) 0 B) 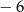− 6 C) 2 D)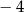 − 4

Rozwiązanie

Jeżeli równanie ma mieć rozwiązanie, to oczywiście musi być: 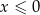x ≤ 0 .

Sposób I

Przekształcamy dane równanie

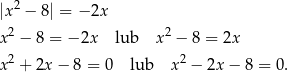
|x2 − 8| = − 2x 2 2 x − 8 = − 2x lub x − 8 = 2x x2 + 2x − 8 = 0 lub x2 − 2x− 8 = 0.

W obu przypadkach 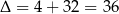Δ = 4+ 32 = 36 i mamy

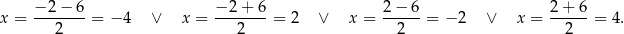
− 2 − 6 − 2 + 6 2− 6 2+ 6 x = ---2--- = − 4 ∨ x = ---2--- = 2 ∨ x = -2---= − 2 ∨ x = --2---= 4.

Jak stwierdziliśmy wcześniej, dodatnie rozwiązania musimy odrzucić i suma pierwiastków jest równa

− 4 − 2 = − 6.

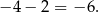
Sposób II

Szkicujemy wykresy obu stron równania

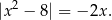
2 |x − 8| = − 2x.

Jeżeli zrobimy to w miarę dokładnie (na papierze w kratkę), to można zgadnąć, że równanie to ma dwa rozwiązania: 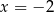x = − 2 i x = − 4 .

PIC

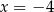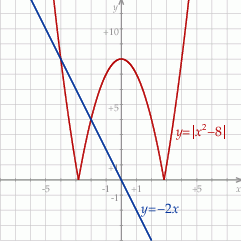
Łatwo sprawdzić to przypuszczenie podstawiając te liczby do równania. Suma pierwiastków jest więc równa

− 2 − 4 = − 6.

 
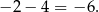
Odpowiedź: B

Wersja PDF