/Szkoła średnia/Zadania testowe

Zadanie nr 1652780

Dodaj do ulubionych
Dodaj do rozwiązanych

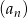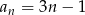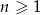Jeżeli ciąg (an) dany jest wzorem an = 3n − 1 dla n ≥ 1 , to suma 10 początkowych wyrazów ciągu 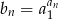a bn = a1n wyraża się wzorem
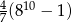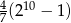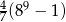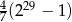
A) 4(8 10 − 1) 7 B) 4(210 − 1 ) 7 C) 4 9 7(8 − 1) D) 4 29 7(2 − 1)

Rozwiązanie

Ponieważ ciąg (an ) jest ciągiem arytmetycznym, to ciąg

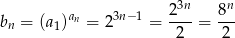
3n n bn = (a1)an = 23n− 1 = 2---= 8-- 2 2

jest ciągiem geometrycznym o pierwszym wyrazie 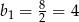8 b1 = 2 = 4 i ilorazie 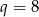q = 8 . Zatem suma jego 10 początkowych wyrazów jest równa

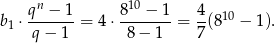
n 10 b ⋅ q-−-1-= 4⋅ 8--−-1-= 4(8 10 − 1). 1 q− 1 8 − 1 7

 
Odpowiedź: A

Wersja PDF